题目内容
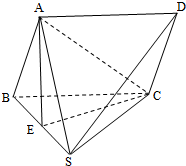 如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.
如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.(1)证明:SD∥平面ACE;
(2)若AB⊥AS,BC=2,求点S到平面ABC的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结BD,交于点F,由已知得EF∥SD,由此能证明SD∥平面ACE.
(2)由已知得AB=
,AE=1,AE⊥CE,CE=
,AC=2,由VS-ABC=VA-SBC,能求出点S到平面ABC的距离.
(2)由已知得AB=
| 2 |
| 3 |
解答:
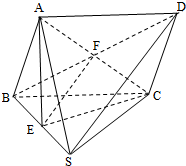 (1)证明:连结BD,交于点F,
(1)证明:连结BD,交于点F,
∵ABCD是平行四边形,∴F是BD的中点,
又∵点E是SB的中点,∴EF∥SD,
∵SD?平面ACE,EF?平面ACE,
∴SD∥平面ACE.
(2)解:∵AB⊥AS,BC=2,且点E是SB的中点,
∴AB=
,AE=1,
又∵AE⊥平面SBC,CE?平面SBC,∴AE⊥CE,
∴侧面SBC是正三角形,∴CE=
,
∴AC=
=2,
∴△ABC是底边为
,腰为2的等腰三角形.
∴S△ABC=
×
×
=
,
设点S一平面ABC的距离为h,
由VS-ABC=VA-SBC,得
h•S△ABC=
AE•S△SBC,
∴h=
=
=
.
 (1)证明:连结BD,交于点F,
(1)证明:连结BD,交于点F,∵ABCD是平行四边形,∴F是BD的中点,
又∵点E是SB的中点,∴EF∥SD,
∵SD?平面ACE,EF?平面ACE,
∴SD∥平面ACE.
(2)解:∵AB⊥AS,BC=2,且点E是SB的中点,
∴AB=
| 2 |
又∵AE⊥平面SBC,CE?平面SBC,∴AE⊥CE,
∴侧面SBC是正三角形,∴CE=
| 3 |
∴AC=
| AE2+CE2 |
∴△ABC是底边为
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
4-
|
| ||
| 2 |
设点S一平面ABC的距离为h,
由VS-ABC=VA-SBC,得
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
| AE•S△SBC |
| S△ABC |
2
| ||
|
2
| ||
| 7 |
点评:本题考查空间点、线、面的位置,考查线线平行、线面平行、线线垂直与线面垂直,考查等积法求几何体的体积,考查空间想象能力、运算能力、逻辑推理能力及化归思想等.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,在复平面内,复数z1和z2对应的点分别是A和B,则z1z2等于( )
如图,在复平面内,复数z1和z2对应的点分别是A和B,则z1z2等于( )| A、-2+i | B、-1+2i |
| C、2-i | D、1+2i |