题目内容
先化简，再求值：
÷(m-1-
)，其中m=
．
| m2-2m+1 |
| m2-1 |
| m-1 |
| m+1 |
| 3 |
考点：有理数指数幂的化简求值
专题：计算题
分析：把原式通分后进行约分计算，然后代入m的值得答案．
解答：
解：
÷(m-1-
)
=
÷
=
•
=
．
∵m=
，
∴
÷(m-1-
)=
=
=
．
| m2-2m+1 |
| m2-1 |
| m-1 |
| m+1 |
=
| (m-1)2 |
| m2-1 |
| (m+1)(m-1)-(m-1) |
| m+1 |
=
| (m-1)2 |
| (m+1)(m-1) |
| m+1 |
| m(m-1) |
| 1 |
| m |
∵m=
| 3 |
∴
| m2-2m+1 |
| m2-1 |
| m-1 |
| m+1 |
| 1 |
| m |
| 1 | ||
|
| ||
| 3 |
点评：本题考查了有理指数幂的化简与求值，是基础的计算题．
练习册系列答案
相关题目
若函数f（x）=x2+a|x-1|（a∈R），则对不同的实数a，函数f（x）的单调区间的个数有可能的是（ ）
| A、1个或2个 |
| B、2个或3个 |
| C、3个或4个 |
| D、2个或4个 |
已知二次函数f（x）=x2-（a-2）x+4是偶函数，则实数a的值为（ ）
| A、0 | B、4 | C、-2 | D、2 |
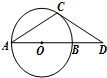（几何证明选讲选做题）如图，已知点D在圆O直径AB的延长线上，过D作圆O的切线，切点为C．若