题目内容
已知二次函数f(x)满足:①在x=1时有极值;②图象过点(0,-3)且在该点处的切线与直线2x+y=0平行.
(1)求f(x)的解析式;
(2)求函数g(x)=f(x+1)的单调递增区间.
(1)求f(x)的解析式;
(2)求函数g(x)=f(x+1)的单调递增区间.
考点:利用导数研究曲线上某点切线方程,函数解析式的求解及常用方法
专题:函数的性质及应用,导数的概念及应用
分析:(1)设f(x)=ax2+bx+c,求导函数,利用极值、导数的几何意义,建立方程组,求出a,b,c,即可求f(x)的解析式;
(2)求出函数g(x)=f(x+1)的解析式,利用导数大于0,可求函数的单调递增区间.
(2)求出函数g(x)=f(x+1)的解析式,利用导数大于0,可求函数的单调递增区间.
解答:
解:(1)设f(x)=ax2+bx+c,
则f'(x)=2ax+b.
由题设可得
即
,
解得:
,
所以f(x)=x2-2x-3;
(2)g(x)=f(x+1)=(x+1)2-2(x+1)-3=x2-4.
令g'(x)=2x>0,得x>0.
故g(x)的单调递增区间为(0,+∞).
则f'(x)=2ax+b.
由题设可得
|
|
解得:
|
所以f(x)=x2-2x-3;
(2)g(x)=f(x+1)=(x+1)2-2(x+1)-3=x2-4.
令g'(x)=2x>0,得x>0.
故g(x)的单调递增区间为(0,+∞).
点评:本题考查导数知识的运用,考查函数的极值,考查导数的几何意义,考查函数的单调性,正确求导是关键.

练习册系列答案
相关题目
已知点P(x,y)的坐标x,y满足
,则x2+y2-4x的取值范围是( )
|
| A、[0,12] |
| B、[-1,12] |
| C、[3,16] |
| D、[-1,16] |
函数y=x3-x2-x的单调递增区间为( )
A、(-∞,-
| ||
B、[-
| ||
C、(-∞,-
| ||
D、[-1,
|
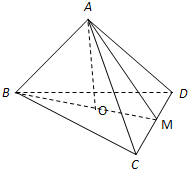 已知正四面体ABCD的棱长为a,点O是△BCD的中心,点M是CD中点.
已知正四面体ABCD的棱长为a,点O是△BCD的中心,点M是CD中点. 如图,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积,(其中∠BAC=30°)
如图,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积,(其中∠BAC=30°)