题目内容
4.△ABC中,角A,B,C的对边分别为a,b,c,2bcosC-c=2a.(Ⅰ)求B的大小;
(Ⅱ)若a=3,且AC边上的中线长为$\frac{{\sqrt{19}}}{2}$,求c的值.
分析 (Ⅰ)由余弦定理化简已知等式可得:a2+c2-b2=-ac,进而可求cosB=-$\frac{1}{2}$,结合范围B∈(0,π),可求B的值.
(Ⅱ)由(Ⅰ)可得:b2=a2+c2+ac=c2+3c+9,取AC中点D,连接BD,由余弦定理可求cosC=$\frac{{a}^{2}+\frac{{b}^{2}}{4}-\frac{19}{4}}{ab}$,整理可得9+b2-c2=2(9+$\frac{{b}^{2}}{4}$-$\frac{19}{4}$),联立即可解得c的值.
解答 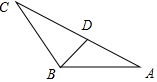 (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)∵2bcosC-c=2a,
∴由余弦定理可得:2b•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$-c=2a,…3分
∴化简可得:a2+c2-b2=-ac,…4分
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=-$\frac{1}{2}$,…5分
∵B∈(0,π),
∴B=$\frac{2π}{3}$.…6分
(Ⅱ)由(Ⅰ)可得:b2=a2+c2+ac=c2+3c+9,①…7分
又∵cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,…8分
取AC中点D,连接BD,在△CBD中,cosC=$\frac{B{C}^{2}+C{D}^{2}-B{D}^{2}}{2BC•CD}$=$\frac{{a}^{2}+\frac{{b}^{2}}{4}-\frac{19}{4}}{ab}$,…9分
∴9+b2-c2=2(9+$\frac{{b}^{2}}{4}$-$\frac{19}{4}$),②…11分
把①代入②,化简可得:c2-3c-10=0,
解得:c=5或c=-2(舍去),可得:c=5.…12分
点评 本题主要考查了正弦定理,余弦定理,两角和与差的三角函数公式等基本知识的应用,考查了运算求解能力,考查了函数与方程思想,化归与转化思想,属于中档题.

| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
| x | 0 | 2 | 4 | 6 |
| y | a | 3 | 5 | 3a |
| A. | $f(x)=sin(\frac{π}{3}x)$ | B. | $f(x)=sin(\frac{π}{2}x)$ | C. | $f(x)=cos(\frac{π}{3}x)$ | D. | $f(x)=cos(\frac{π}{2}x)$ |
| A. | $\frac{7}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
| A. | $({-∞,-\frac{1}{e}})$ | B. | (-∞,-e) | C. | (e,+∞) | D. | $({\frac{1}{e},+∞})$ |
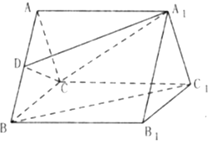 如图,在三棱柱ABC-A1B1C1中,侧棱垂直底面,各棱长均为2,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直底面,各棱长均为2,D为AB的中点.