题目内容
14.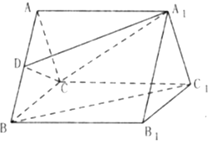 如图,在三棱柱ABC-A1B1C1中,侧棱垂直底面,各棱长均为2,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直底面,各棱长均为2,D为AB的中点.(1)求证:BC1∥平面A1CD;
(2)求证:平面A1CD⊥平面ABB1A1
(3)求A1B1与平面A1CD所成角的正切值.
分析 (1)连结AC1,设AC1与A1C相交于点E,连接DE,则DE∥BC1,由此能证明BC1∥平面A1CD.
(2)推导出CD⊥AA1,CD⊥AB,从而CD⊥面ABB1A1,由此能证明平面A1CD⊥平面ABB1A1.
(3)作B1E⊥A1D于E,则∠B1A1E为所A1B1与平面A1CD所成角,由此能求出A1B1与平面A1CD所成角的正切值.
解答 证明:(1)连结AC1,设AC1与A1C相交于点E,连接DE,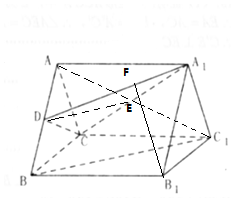
∵在三棱柱ABC-A1B1C1中,CC1A1A是平行四边形,
∴E为AC1中点,
∵D为AB的中点,∴DE∥BC1,
∵BC1?平面A1CD,DE?平面A1CD,
∴BC1∥平面A1CD.…(4分)
(2)∵A1A⊥平面ABC,CD?平面ABC,
∴CD⊥AA1,
又∵CD⊥AB,AB∩AA1=A,AB,A1A?面ABB1A1,
∴CD⊥面ABB1A1,
∵CD?面A1CD,∴平面A1CD⊥平面ABB1A1.…(8分)
解:(3)作B1F⊥A1D于F,
由(2)知B1F⊥面A1DC,
∴∠B1A1F为所A1B1与平面A1CD所成角,
tan∠B1A1F=tan∠ADA1=2,
∴A1B1与平面A1CD所成角的正切值为2.…(13分)
点评 本题考查线面平行、面面垂直的证明,考查线面角的正切值求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.为了研究某学科成绩是否在学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分)

(Ⅰ)求男生和女生的平均成绩
(Ⅱ)请根据图示,将2×2列联表补充完整,并根据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅲ)用分层抽样的方法从男生和女生中抽取5人进行学习问卷调查,并从5人中选取两名学生对该学科进行考后重测,求至少有一名女生的概率
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$

(Ⅰ)求男生和女生的平均成绩
(Ⅱ)请根据图示,将2×2列联表补充完整,并根据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
| 优分 | 非优分 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 50 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k2) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 0.46 | 0.71 | 1.32 | 2.07 | 2.71 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
19.已知集合$P=\{x|y=\sqrt{2-x}\}$,Q={x|y=ln(x+1)},则P∩Q=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x≤2} | D. | {x|-1<x<2} |
6.点P为棱长是2的正方体ABCD-A1B1C1D1的内切球O球面上的动点,点M为B1C1的中点,若满足DP⊥BM,则动点P的轨迹的长度为( )
| A. | $\frac{{\sqrt{5}π}}{5}$ | B. | $\frac{{2\sqrt{5}π}}{5}$ | C. | $\frac{{4\sqrt{5}π}}{5}$ | D. | $\frac{{8\sqrt{5}π}}{5}$ |
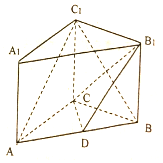 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.