题目内容
9.在△ABC中,若A=60°,b=8,S△ABC=12$\sqrt{3}$,则a=2$\sqrt{13}$.分析 由已知利用三角形面积公式可求c的值,进而利用余弦定理即可解得a的值.
解答 解:∵A=60°,b=8,S△ABC=12$\sqrt{3}$=$\frac{1}{2}$bcsinA=$\frac{1}{2}×8×c×\frac{\sqrt{3}}{2}$,
∴解得:c=6,
∴利用余弦定理可得:a=$\sqrt{{b}^{2}+{c}^{2}-2bccosA}$=$\sqrt{{8}^{2}+{6}^{2}-2×8×6×\frac{1}{2}}$=2$\sqrt{13}$.
故答案为:2$\sqrt{13}$.
点评 本题主要考查了三角形面积公式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
20.已知函数f(x)=$\frac{a}{x}-{e^{-x}}(a∈R$且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
| A. | (0,$\frac{1}{e}$] | B. | (一∞,$\frac{1}{e}$] | C. | (0,$\frac{1}{e}$) | D. | (一∞,$\frac{1}{e}$) |
17.若公差为2的等差数列{an}的前9项和为81,则a9=( )
| A. | 1 | B. | 9 | C. | 17 | D. | 19 |
14.某几何体的三视图如图所示,该几何体四个面中,面积最大的面积是( )


| A. | 8 | B. | 10 | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
1.函数f(x)=$\frac{1}{2}$sin2xtanx+2sinxtan$\frac{x}{2}$的值域为( )
| A. | [0,4] | B. | [0,4) | C. | [0,3)∪(3,4] | D. | [0,3)∪(3,4) |
18.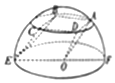 如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
 如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{4\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
19.已知集合$P=\{x|y=\sqrt{2-x}\}$,Q={x|y=ln(x+1)},则P∩Q=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x≤2} | D. | {x|-1<x<2} |