题目内容
19.执行如图所示的程序框图,若输入n=2017,输出S的值为0,则f(x)的解析式可以是( )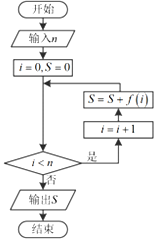
| A. | $f(x)=sin(\frac{π}{3}x)$ | B. | $f(x)=sin(\frac{π}{2}x)$ | C. | $f(x)=cos(\frac{π}{3}x)$ | D. | $f(x)=cos(\frac{π}{2}x)$ |
分析 模拟程序的运行,可得程序框图的功能是计算并输出S=f(1)+f(2)+…+f(2017)的值,由S=f(1)+f(2)+…+f(2017)=0,观察四个选项,利用正弦函数,余弦函数值的周期性即可计算得解.
解答 解:模拟程序的运行,可得程序框图的功能是计算并输出S=f(1)+f(2)+…+f(2017)的值,
由于S=f(1)+f(2)+…+f(2017)=0,
观察四个选项,相位为$\frac{π}{3}x$的三角函数的最小正周期为$\frac{2π}{{\frac{π}{3}}}=6$,
对于选项A:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=336(f(1)+f(2)+…++f(6))+f(2017)\\=f(2017)=f(1)=sin\frac{π}{3}≠0\end{array}$
故排除;
选项C:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=336(f(1)+f(2)+…++f(6))+f(2017)\\=f(2017)=f(1)=cos\frac{π}{3}≠0\end{array}$
故排除;
由于,相位为$\frac{π}{2}x$的三角函数的最小正周期为$\frac{2π}{{\frac{π}{2}}}=4$,
选项B:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=504(f(1)+f(2)+…++f(4))+f(2017)\\=f(2017)=f(1)=sin\frac{π}{2}≠0\end{array}$,
故排除.
选项D:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=504(f(1)+f(2)+…++f(4))+f(2017)\\=f(2017)=f(1)=cos\frac{π}{2}=0\end{array}$
故正确.
故选:D.
点评 本题主要考查了循环结构的程序框图的应用,考查了正弦函数,余弦函数的周期性,模拟程序的运行得程序框图的功能是解题的关键,属于基础题.

| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 3$\sqrt{5}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{1}{5}$ |