题目内容
已知a＞0，b＞0，且
+
≤a，
+
≤b，则
+
的最大值为 ．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
考点：基本不等式
专题：不等式的解法及应用
分析：由已知不妨设0＜a≤b，可得
≥
＞0，于是
+
≤
，且
+
≤a，
+
≤b，得到
+
≤[
，a，b]min，解出即可．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 2 |
| a |
解答：
解：由a＞0，b＞0，且
+
≤a，
+
≤b，
不妨设0＜a≤b，
则
≥
＞0，
∴
+
≤
，且
+
≤a，
+
≤b，
∴
+
≤[
，a，b]min，
可得
≤a，解得a≥
．
因此
+
的最大值为
．
故答案为：
．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
不妨设0＜a≤b，
则
| 1 |
| a |
| 1 |
| b |
∴
| 1 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
∴
| 1 |
| a |
| 1 |
| b |
| 2 |
| a |
可得
| 2 |
| a |
| 2 |
因此
| 1 |
| a |
| 1 |
| b |
| 2 |
故答案为：
| 2 |
点评：本题考查了不等式的性质及其解法，考查了推理能力和计算能力，属于难题．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
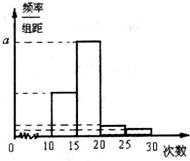对山东省实验中学高三年级学生参加社区服务次数进行统计，随机抽取m名学生作样本，得到这M名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表和频率分布直方图如图：设an是(1-
)n的展开式中x项的系数（n=2，3，4，…），若bn=
，则bn的最大值是（ ）
| x |
| an+1 | ||
(n+7)
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|