题目内容
 如图,菱形ABCD与矩形BDEF所在平面互相垂直,∠BAD=
如图,菱形ABCD与矩形BDEF所在平面互相垂直,∠BAD=| π |
| 3 |
(Ⅰ)求证:FC∥平面AED;
(Ⅱ)若BF=k•BD,当二面角A-EF-C为直二面角时,求k的值;
(Ⅲ)在(Ⅱ)的条件下,求直线BC与平面AEF所成的角θ的正弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)通过证明平面FBC∥平面EDA,即可证明FC∥平面AED;
(Ⅱ)取EF,BD的中点M,N.说明∠AMC就是二面角A-EF-C的平面角,利用二面角A-EF-C为直二面角,即可求k的值;
(Ⅲ)在(Ⅱ)的条件下,求直线BC与平面AEF所成的角θ的正弦值.
几何方法:由(Ⅱ)CM⊥平面AEF,欲求直线BC与平面AEF所成的角,先求BC与MC所成的角,连结BM,设BC=2.
则在△MBC中,求解即可
(Ⅲ)向量方法:
以D为原点,DC为y轴、DE为z轴建立如图的直角坐标系,设AD=2.求出平面AEF的法向量
=
=(-
,
,-
),通过cos?
,
>=
=-
.然后求解即可.
(Ⅱ)取EF,BD的中点M,N.说明∠AMC就是二面角A-EF-C的平面角,利用二面角A-EF-C为直二面角,即可求k的值;
(Ⅲ)在(Ⅱ)的条件下,求直线BC与平面AEF所成的角θ的正弦值.
几何方法:由(Ⅱ)CM⊥平面AEF,欲求直线BC与平面AEF所成的角,先求BC与MC所成的角,连结BM,设BC=2.
则在△MBC中,求解即可
(Ⅲ)向量方法:
以D为原点,DC为y轴、DE为z轴建立如图的直角坐标系,设AD=2.求出平面AEF的法向量
| n |
| MC |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| n |
| CB |
| ||||
|
|
| ||
| 4 |
解答:
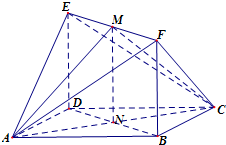 解:(Ⅰ)证明:∵FB∥ED,BC∥AD,∴平面FBC∥平面EDA.
解:(Ⅰ)证明:∵FB∥ED,BC∥AD,∴平面FBC∥平面EDA.
故FC∥平面AED----------------(5分)
(Ⅱ)取EF,BD的中点M,N.由于AE=AF,CE=CF,
所以AM⊥EF,CM⊥EF,∠AMC就是二面角A-EF-C的平面角-------(8分)
当二面角A-EF-C为直二面角时,MN=AN=
BD,即k=
.---(10分)
(Ⅲ)几何方法:
由(Ⅱ)CM⊥平面AEF,欲求直线BC与平面AEF所成的角,先求BC与MC所成的角.--------(12分)
连结BM,设BC=2.
则在△MBC中,CM=
MN=
•
=
,MB=2,
cos∠MCB=
=-
.
∴sinθ=
.----------------(14分)
(Ⅲ)向量方法:
以D为原点,DC为y轴、DE为z轴
建立如图的直角坐标系,设AD=2.
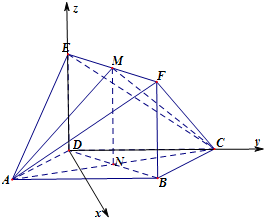
则M(
,
,
),C(0,2,0),平面AEF的法向量
=
=(-
,
,-
),-------(12分)
=
=(
,-1,0).cos?
,
>=
=-
.∴sinθ=
.---------------(14分)
注:用常规算法求法向量,或建立其它坐标系计算的,均参考以上评分标准给分
 解:(Ⅰ)证明:∵FB∥ED,BC∥AD,∴平面FBC∥平面EDA.
解:(Ⅰ)证明:∵FB∥ED,BC∥AD,∴平面FBC∥平面EDA.故FC∥平面AED----------------(5分)
(Ⅱ)取EF,BD的中点M,N.由于AE=AF,CE=CF,
所以AM⊥EF,CM⊥EF,∠AMC就是二面角A-EF-C的平面角-------(8分)
当二面角A-EF-C为直二面角时,MN=AN=
| ||
| 2 |
| ||
| 2 |
(Ⅲ)几何方法:
由(Ⅱ)CM⊥平面AEF,欲求直线BC与平面AEF所成的角,先求BC与MC所成的角.--------(12分)
连结BM,设BC=2.
则在△MBC中,CM=
| 2 |
| 2 |
| 3 |
| 6 |
cos∠MCB=
| MC2+BC2-MB2 |
| 2MC•BC |
| ||
| 4 |
∴sinθ=
| ||
| 4 |
(Ⅲ)向量方法:
以D为原点,DC为y轴、DE为z轴
建立如图的直角坐标系,设AD=2.

则M(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| n |
| MC |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| CB |
| DA |
| 3 |
| n |
| CB |
| ||||
|
|
| ||
| 4 |
| ||
| 4 |
注:用常规算法求法向量,或建立其它坐标系计算的,均参考以上评分标准给分
点评:本题考查直线与平面平行的判断方法,二面角的平面角的应用与求法,直线与平面所成角的求法,考查空间想象能力以及计算能力,转化思想的应用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
若方程|2x-2|-a=0有两个解,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,2) | D、∅ |
