题目内容
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
考点:用空间向量求直线与平面的夹角,直线与平面所成的角
专题:空间角,空间向量及应用
分析:可以考虑用向量解决本题,所以分别以DA,DC,DD1三直线为x轴,y轴,z轴建立空间直角坐标系,根据线面角的概念知D1C1与平面A1BC1所成角的正弦值等于
与平面A1BC1的法向量夹角的余弦值的绝对值,所以根据已知的边的长度求出
,
,
的坐标,设平面A1BC1的法向量为
=(x,y,z),根据向量
与
,
垂直即可求出
,根据向量夹角余弦公式即可求出向量
,
夹角的余弦值的绝对值.
| D1C1 |
| D1C1 |
| A1C1 |
| A1B |
| n |
| n |
| A1C1 |
| A1B |
| n |
| D1C1 |
| n |
解答:
解:如图,分别以DA,DC,DD1三条边所在直线为x轴,y轴,z轴建立空间直角坐标系;
 根据题意知,D1C1与平面A1BC1所成角的正弦值等于向量
根据题意知,D1C1与平面A1BC1所成角的正弦值等于向量
和平面A1BC1的法向量夹角余弦值的绝对值;
根据已知的边的长度,可求以下几点坐标:
D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0);
∴
=(0,2,0),
=(-1,2,0),
=(0,2,-1);
设平面A1BC1的法向量为
=(x,y,z),则
;
∴
,取y=1,∴
=(2,1,2);
∴|cos<
,
>|=|
|=|
|=
.
故选A.
 根据题意知,D1C1与平面A1BC1所成角的正弦值等于向量
根据题意知,D1C1与平面A1BC1所成角的正弦值等于向量| D1C1 |
根据已知的边的长度,可求以下几点坐标:
D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0);
∴
| D1C1 |
| A1C1 |
| A1B |
设平面A1BC1的法向量为
| n |
|
∴
|
| n |
∴|cos<
| D1C1 |
| n |
| ||||
|
|
| 2 |
| 2×3 |
| 1 |
| 3 |
故选A.
点评:考查运用空间向量解决线面角的问题,以及向量数量积的坐标公式,两向量夹角的余弦公式.

练习册系列答案
相关题目
设复数z=
,
是z的共轭复数,则z+
=( )
| 1 |
| 1-i |
. |
| z |
. |
| z |
A、
| ||
| B、i | ||
| C、-1 | ||
| D、1 |
已知全集U=R,集合A={x|x<-2,或x>0},B={x|
<1},则(∁UA)∩B=( )
| 1 |
| x |
| A、(-2,0) | B、[-2,0) |
| C、∅ | D、(-2,1) |
已知集合A={x|x+1<0},B={x|x-3<0},那么集合A∪B等于( )
| A、{x|x<-3} |
| B、{x|x<3} |
| C、{x|x<-1} |
| D、{x|-1<x<3} |
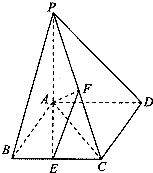 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角为45°,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角为45°,E、F分别是BC、PC的中点. 如图,菱形ABCD与矩形BDEF所在平面互相垂直,∠BAD=
如图,菱形ABCD与矩形BDEF所在平面互相垂直,∠BAD=