题目内容
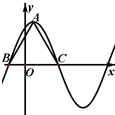 函数f(x)=2
函数f(x)=2| 3 |
| π |
| 2 |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:计算题
分析:结合函数的图象与解析式可以得出A点的纵坐标,即为三解形ABC的高,从而能求出周期,进而求出ω,利利三角函数的定义结合φ的范围求出φ的值.
解答:
解:结合函数f(x)=2
sin(ωx+φ)的解析式与图象可知A点的纵坐标为2
,
∴正三角形ABC的高为2
,
∴BC=4,即函数的周期T=
=8,解得ω=
,
∵φ的终边经过点(1,
),
∴由三角函数的定义可知,tanφ=
,
又∵0<φ<
,∴φ=
,
故答案为:ω=
,φ=
.
| 3 |
| 3 |
∴正三角形ABC的高为2
| 3 |
∴BC=4,即函数的周期T=
| 2π |
| ω |
| π |
| 4 |
∵φ的终边经过点(1,
| 3 |
∴由三角函数的定义可知,tanφ=
| 3 |
又∵0<φ<
| π |
| 2 |
| π |
| 3 |
故答案为:ω=
| π |
| 4 |
| π |
| 3 |
点评:本题考查了三解函数的定义及根据图象求解析式的方法;关键是找到题目的突破点A点的纵坐标是三解形的高.

练习册系列答案
相关题目
已知等比数列{an}的各项均为正数,对k∈N*,akak+5=a,ak+10ak+15=b,则ak+15ak+20=( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|