题目内容
8.已知π<α<$\frac{3π}{2}$,sinα=-$\frac{4}{5}$.(Ⅰ)求cosα的值;
(Ⅱ)求sin2α+3tanα的值.
分析 (Ⅰ)由已知利用同角三角函数基本关系式即可化简取值得解.
(Ⅱ)利用倍角公式,同角三角函数基本关系式化简所求即可计算得解.
解答 (本题满分13分)
解:(Ⅰ)因为π<α<$\frac{3π}{2}$,sinα=-$\frac{4}{5}$,
故cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{3}{5}$.-------------------------------------------------(6分)
(Ⅱ)sin2α+3tanα=2sinαcosα+3×$\frac{sinα}{cosα}$=2×(-$\frac{4}{5}$)×(-$\frac{3}{5}$)+3×$\frac{(-\frac{4}{5})}{(-\frac{3}{5})}$=4$\frac{24}{25}$.-------------------------------------(13分)
点评 本题主要考查了倍角公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
19.若实数x,y∈R,则“x>0,y>0”是“xy>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.抛物线y2=2x的准线方程是( )
| A. | x=$\frac{1}{2}$ | B. | x=1 | C. | x=-$\frac{1}{2}$ | D. | x=-1 |
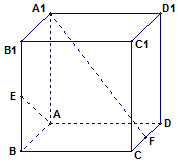 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.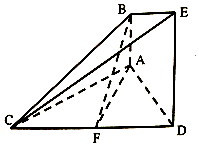 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.