题目内容
20.过点P(-1,0)作直线与抛物线y2=8x相交于A,B两点,且2|PA|=|AB|,则点B到该抛物线焦点的距离为5.分析 利用过P(-1,0)作直线与抛物线y2=8x相交于A,B两点,且2|PA|=|AB|,求出B的横坐标,即可求出点B到抛物线的焦点的距离.
解答 解:设A(x1,y1),B(x2,y2),设A,B在直线x=-1的射影分别为D,E.
∵2|PA|=|AB|,
∴3(x1+1)=x2+1即3x1+2=x2,3y1=y2,
∵A.B两点在抛物线y2=8x上
∴3$\sqrt{8{x}_{1}}$=$\sqrt{8(3{x}_{1}+2)}$,
解得x1=$\frac{1}{3}$,x2=3,
∴点B到抛物线的焦点的距离为BF=3+2=5.
故答案为5
点评 本题考查抛物线的定义,考查学生的计算能力,解题的关键是利用抛物线的定义确定B的横坐标.

练习册系列答案
相关题目
11.在空间,可以确定一个平面的条件是( )
| A. | 两条直线 | B. | 一点和一条直线 | C. | 三个点 | D. | 一个三角形 |
10.设复数z满足z(1+i)=i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
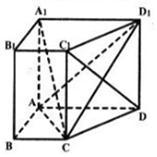 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中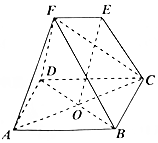 如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.
如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.