题目内容
18.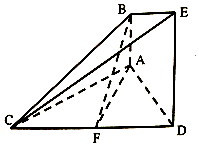 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.(1)求证:AF∥平面BCE;
(2)求A到平面BCE的距离.
分析 (1)通过取CE的中点G,利用三角形的中位线定理和平行四边形的性质及线面平行的判定定理即可证明;
(2)利用三棱锥的体积公式计算,即可求A到平面BCE的距离.
解答 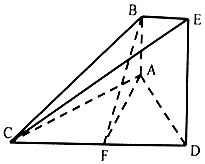 (1)证明:取CE的中点G,连接FG、BG.
(1)证明:取CE的中点G,连接FG、BG.
∵F为CD的中点,∴GF∥DE且$GF=\frac{1}{2}DE$.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB,
又$AB=\frac{1}{2}DE$,∴GF=AB.
∴四边形GFAB为平行四边形,则AF∥BG.
∵AF?平面BCE,BG?平面BCE,∴AF∥平面BCE.
(2)连接AE,设A到平面BCE的距离为h,
在△BCE中,$BC=BE=\sqrt{5}$,$CE=2\sqrt{2}$,
∴${S_{△BCE}}=\frac{1}{2}×2\sqrt{2}×\sqrt{3}=\sqrt{6}$,
又$CH=\sqrt{3}$,${S_{△ABE}}=\frac{1}{2}×1×2=1$,
∴由VA-BCE=VC-ABE,即$\frac{1}{3}•h•{S_{△BCE}}=\frac{1}{3}•CH•{S_{△ABE}}$(CH为正△ACD的高),
∴$h=\frac{{\sqrt{2}}}{2}$
即点A到平面BCE的距离为$\frac{{\sqrt{2}}}{2}$.
点评 熟练掌握线面平行的判定定理和性质定理及棱锥的体积计算公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.用三段论推理:“任何实数的绝对值大于0,因为a是实数,所以a的绝对值大于0”,你认为这个推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 是正确的 |
3.若直线mx+2y+m=0与直线3mx+(m-1)y+7=0平行,则m的值为( )
| A. | 7 | B. | 0或7 | C. | 0 | D. | 4 |
10.设复数z满足z(1+i)=i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
7.将函数f(x)=sin2x的图象向右平移φ$({0<φ<\frac{π}{2}})$个单位后得到函数g(x)的图象,若g(x)在区间$[{0,\frac{π}{6}}]$上单调递增,且函数g(x)的最大负零点在区间$({-\frac{π}{3},-\frac{π}{6}})$上,则φ的取值范围是( )
| A. | [$\frac{π}{12}$,$\frac{π}{4}$] | B. | [$\frac{π}{6}$,$\frac{5π}{12}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{6}$,$\frac{π}{4}$] |