题目内容
18.已知数列{an}的前n项和Sn=n2+pn,且a2,a5,a10成等比数列.(1)求数列{an}的通项公式;
(2)若bn=1+$\frac{5}{{a}_{n}•{a}_{n+1}}$,求数列{bn}的前n项和Tn.
分析 (1)根据数列的递推公式可得an=2n-1+p,再根据a2,a5,a10成等比数列,求出p的值,问题得以解决,
(2)把(1)求出的an代入bn,再求出bn的表达式,然后由裂项相消法来求数列{bn}的前n项和Tn.
解答 解:(1)当n≥2时,an=Sn-Sn-1=2n-1+p,
当n=1时,a1=S1=1+p,也满足,
故an=2n-1+p,
∵a2,a5,a10成等比数列,
∴(3+p)(19+p)=(9+p)2,
∴p=6,
∴an=2n+5,
(2)由(1)可得bn=$\frac{4{n}^{2}+24n+40}{{a}_{n}•{a}_{n+1}}$=$\frac{(2n+5)(2n+7)+5}{(2n+5)(2n+7)}$=$\frac{5}{2}$($\frac{1}{2n+5}$-$\frac{1}{2n+7}$)+1,
∴Tn=n+$\frac{5}{2}$($\frac{1}{7}$-$\frac{1}{9}$+$\frac{1}{9}$-$\frac{1}{11}$+…+$\frac{1}{2n+5}$-$\frac{1}{2n+7}$)=n+$\frac{5n}{14n+49}$=$\frac{14{n}^{2}+54n}{14n+49}$
点评 本题考查了等差数列的通项公式及等比数列的性质以及裂项求和,考查了基础知识和运算能力,属于中档题

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.已知A是抛物线M:y2=2px(p>0)与圆C在第一象限的公共点,其中圆心C(0,4),点A到M的焦点F的距离与C的半径相等,M上一动点到其准线与到点C的距离之和的最小值等于C的直径,O为坐标原点,则直线OA被圆C所截得的弦长为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{7\sqrt{2}}{6}$ | D. | $\frac{7\sqrt{2}}{3}$ |
13.命题p:?x∈R,tanx>1,命题q:抛物线y=$\frac{1}{3}$x2的焦点到准线的距离为$\frac{1}{6}$,那么下列命题为真命题的是( )
| A. | ¬p | B. | (¬p)∨q | C. | p∧q | D. | p∧(¬q) |
3.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0,}&{\;}\\{x-y-1≤0,}&{\;}\\{x-1≥0.}&{\;}\end{array}\right.$若a∈[-2,9],则z=ax+y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值的概率为( )
| A. | $\frac{9}{11}$ | B. | $\frac{7}{11}$ | C. | $\frac{6}{11}$ | D. | $\frac{5}{11}$ |
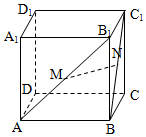 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.