题目内容
17.已知f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数x满足f(log${\;}_{\frac{1}{2}}$|x+1|)<f(-1),则x的取值范围是$(-3,-\frac{3}{2})∪(-\frac{1}{2},1)$.分析 利用函数是偶函数得到不等式f(log${\;}_{\frac{1}{2}}$|x+1|)<f(-1),等价为f(|log2|x+1||)<f(1),然后利用函数在区间[0,+∞)上单调递增即可得到不等式的解集.
解答 解:∵函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.
∴不等式f(log${\;}_{\frac{1}{2}}$|x+1|)<f(-1),等价为f(|log2|x+1||)<f(1),
即|log2|x+1||<1
∴-1<log2|x+1|<1,
解得x的取值范围是$(-3,-\frac{3}{2})∪(-\frac{1}{2},1)$.
故答案为$(-3,-\frac{3}{2})∪(-\frac{1}{2},1)$.
点评 本题主要考查函数奇偶性和单调性的应用,利用函数是偶函数的性质得到f(a)=f(|a|)是解决偶函数问题的关键.

练习册系列答案
相关题目
6.用三段论推理:“任何实数的绝对值大于0,因为a是实数,所以a的绝对值大于0”,你认为这个推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 是正确的 |
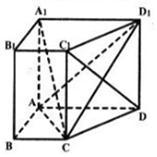 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中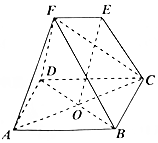 如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.
如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.