题目内容
18.记min{a,b,c}为实数a,b,c中最小的一个,已知函数f(x)=-x+1图象上的点(x1,x2+x3)满足:对一切实数t,不等式-t2-${2}^{{x}_{1}^{2}}$t-2${\;}^{2+{x}_{1}^{2}-{x}_{2}^{2}-{x}_{3}^{2}}$+4${\;}^{2-{x}_{2}^{2}-{x}_{3}^{2}}$≤0均成立,如果min{-x1,-x2,-x3}=-x1,那么x1的取值范围是$[\frac{1}{3},+∞)$.分析 函数f(x)=-x+1图象上的点(x1,x2+x3),可得x2+x3=-x1+1.由于min{-x1,-x2,-x3}=-x1,可得-x2>-x1,-x3≥-x1,可得x1$≥\frac{1}{3}$.对一切实数t,不等式-t2-${2}^{{x}_{1}^{2}}$t-2${\;}^{2+{x}_{1}^{2}-{x}_{2}^{2}-{x}_{3}^{2}}$+4${\;}^{2-{x}_{2}^{2}-{x}_{3}^{2}}$≤0均成立,可得△≤0,化为:$({2}^{{x}_{1}^{2}}-{2}^{3-{x}_{2}^{2}-{x}_{3}^{2}})^{2}$≤0,解出即可得出.
解答 解:函数f(x)=-x+1图象上的点(x1,x2+x3),∴x2+x3=-x1+1.
∵min{-x1,-x2,-x3}=-x1,∴-x2>-x1,-x3≥-x1,∴x2≤x1,x3≤x1,∴-x1+1≤2x1,解得x1$≥\frac{1}{3}$.
对一切实数t,不等式-t2-${2}^{{x}_{1}^{2}}$t-2${\;}^{2+{x}_{1}^{2}-{x}_{2}^{2}-{x}_{3}^{2}}$+4${\;}^{2-{x}_{2}^{2}-{x}_{3}^{2}}$≤0均成立,
∴△=$(-{2}^{{x}_{1}^{2}})^{2}$+4(4${\;}^{2-{x}_{2}^{2}-{x}_{3}^{2}}$-2${\;}^{2+{x}_{1}^{2}-{x}_{2}^{2}-{x}_{3}^{2}}$)≤0,
化为:$({2}^{{x}_{1}^{2}}-{2}^{3-{x}_{2}^{2}-{x}_{3}^{2}})^{2}$≤0,
∴${x}_{1}^{2}$≤$3-{x}_{2}^{2}$-${x}_{3}^{2}$,或${x}_{1}^{2}$≥$3-{x}_{2}^{2}$-${x}_{3}^{2}$,
∵x2+x3=-x1+1,
∴2(${x}_{2}^{2}+{x}_{3}^{2}$)≥$({x}_{2}+{x}_{3})^{2}$=$(1-{x}_{1})^{2}$,
∴${x}_{1}^{2}$≤$3-{x}_{2}^{2}$-${x}_{3}^{2}$≤3-$\frac{1}{2}$$(1-{x}_{1})^{2}$,及x1$≥\frac{1}{3}$,解得$\frac{1}{3}$≤x1≤$\frac{5}{3}$.
或${x}_{1}^{2}$≥$3-{x}_{2}^{2}$-${x}_{3}^{2}$,则${x}_{1}^{2}$+${x}_{2}^{2}$+${x}_{3}^{2}$-3≥${x}_{1}^{2}$+$\frac{1}{2}$$(1-{x}_{1})^{2}$-3≥0,及x1$≥\frac{1}{3}$,解得${x}_{1}≥\frac{5}{3}$.
综上可得:x1的取值范围是$[\frac{1}{3},+∞)$.
故答案为:$[\frac{1}{3},+∞)$.
点评 本题考查了一元二次不等式的解集与判别式的关系、不等式的性质、基本不等式的性质,考查了推理能力与计算能力,属于难题.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | a>1 | B. | 0<a<1 | C. | a≥0 | D. | a>0 |
| A. | 4 | B. | $\frac{4}{sin1}$ | C. | 4sin1 | D. | sin2 |
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
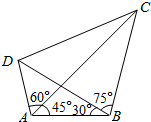 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.