题目内容
19.下列各组函数表示同一函数的是( )①f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x(x≥0)}\\{-x(x<0)}\end{array}\right.$ ②f(x)=$\frac{{x}^{2}-4}{x-2}$,g(x)=x+2 ③f(x)=$\sqrt{{x}^{2}}$,g(x)=x+2 ④f(x)=$\sqrt{1-{x}^{2}}$+$\sqrt{{x}^{2}-1}$,g(x)=0,x∈{-1,1}.
| A. | ①③ | B. | ① | C. | ②④ | D. | ①④ |
分析 通过去绝对值号,求函数的定义域,以及化简函数解析式便可判断f(x)和g(x)的对应法则和定义域是否都相同,从而找出表示同一函数的序号.
解答 解:①$f(x)=|x|=\left\{\begin{array}{l}{x}&{x≥0}\\{-x}&{x<0}\end{array}\right.$,∴这两个函数为同一函数;
②f(x)的定义域为{x|x≠2},g(x)的定义域为R,∴这两个函数不是同一函数;
③f(x)=|x|,g(x)=x+2,这两个函数的对应法则不同,不是同一函数;
④解$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{{x}^{2}-1≥0}\end{array}\right.$得,x2=1,∴x=±1;
∴f(x)=0,x∈{-1,1};
∴这两个函数为同一函数;
∴表示同一函数的为①④.
故选:D.
点评 考查函数的三要素:定义域,值域和对应法则,而由定义域和对应法则即可确定一个函数,从而得到判断两函数是否为同一函数的方法:求定义域,化简函数解析式.

练习册系列答案
相关题目
9.若二次函数y=x2+mx+4的图象与x轴没有公共点,则实数m的取值范围是( )
| A. | (-4,4) | B. | [-4,4] | C. | (-∞,-4)∪(4,+∞) | D. | (-∞,-4]∪[4,+∞) |
7.已知函数f(x)=(x+6)(x-7),g(x)=ax2-(3a+1)x+3,其中a<0,若存在6个整数x0,有f(x0)<0与g(x0)<0同时成立,则a的值可能为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{3}$ | D. | -4 |
14.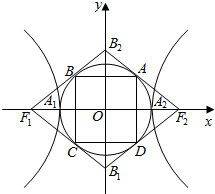 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{\sqrt{5}+2}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}-2}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
1.已知f(x)是定义域为R的奇函数,若?x∈R,f′(x)>-2,则不等式f(x-1)<x2(3-2lnx)+3(1-2x)的解集是( )
| A. | (0,1) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,1) |
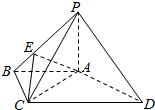 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.