题目内容
13．已知f（x）=$\frac{{2}^{x}+2a-1}{{2}^{x}+1}$的值域为（$\frac{1}{2}$，1），则实数a的值为$\frac{3}{4}$．分析 分离常数法化简f（x）=$\frac{{2}^{x}+2a-1}{{2}^{x}+1}$=1+$\frac{2a-2}{{2}^{x}+1}$，从而可得0＜$\frac{2-2a}{{2}^{x}+1}$＜$\frac{1}{2}$，从而解得．
解答 解：∵f（x）=$\frac{{2}^{x}+2a-1}{{2}^{x}+1}$
=1+$\frac{2a-2}{{2}^{x}+1}$∈（$\frac{1}{2}$，1），
∴0＜$\frac{2-2a}{{2}^{x}+1}$＜$\frac{1}{2}$，
∴2-2a=$\frac{1}{2}$，
∴a=$\frac{3}{4}$；
故答案为：$\frac{3}{4}$．
点评 本题考查了分离常数法的应用及函数的值域的求法应用．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14．
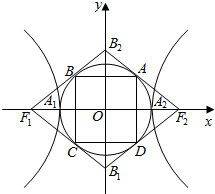我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线．如图，黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2，若以A1，A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D，则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=（ ）
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线．如图，黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2，若以A1，A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D，则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | $\frac{\sqrt{5}+2}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\frac{\sqrt{5}-2}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
1．已知f（x）是定义域为R的奇函数，若?x∈R，f′（x）＞-2，则不等式f（x-1）＜x2（3-2lnx）+3（1-2x）的解集是（ ）
| A． | （0，1） | B． | （1，+∞） | C． | （$\frac{1}{2}$，+∞） | D． | （$\frac{1}{2}$，1） |
