题目内容
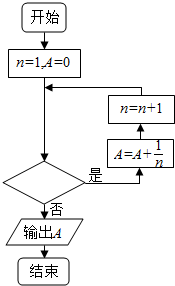
7.已知函数$f(x)=kx-(k+1)lnx-\frac{1}{x}$.(Ⅰ)当$k=\frac{1}{2}$时,求函数f(x)的单调区间和极值;
(Ⅱ)求证:当0<k<1时,关于x的不等式f(x)>1在区间[1,e]上无解.(其中e=2.71828…)
分析 (Ⅰ)当$k=\frac{1}{2}$时,化简函数f(x)的解析式,利用函数的导数求解函数的单调区间和极值;
(Ⅱ)当0<k<1时,求出函数f(x)在区间[1,e]上的最大值,然后判断结果即可.
解答 解:(Ⅰ)因为$f(x)=kx-(k+1)lnx-\frac{1}{x}$,
所以$f'(x)=k-\frac{k+1}{x}+\frac{1}{x^2}=\frac{{k{x^2}-(k+1)x+1}}{x^2}$,….(1分)
当$k=\frac{1}{2}$时,$f'(x)=\frac{{\frac{1}{2}(x-2)(x-1)}}{x^2}$.….(2分)
令$f'(x)=\frac{{\frac{1}{2}(x-2)(x-1)}}{x^2}=0$,得x1=1,x2=2,….(3分)
所以f′(x),f(x)随x的变化情况如下表:
| x | (0,1) | 1 | (1,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以f(x)在x=1处取得极大值$f(1)=-\frac{1}{2}$,
在x=2处取得极小值$f(2)=\frac{1}{2}-\frac{3}{2}ln2$.….(7分)
函数f(x)的单调递增区间为(0,1),(2,+∞),f(x)的单调递减区间为(1,2).….(8分)
(Ⅱ)证明:不等式f(x)>1在区间[1,e]上无解,等价于f(x)≤1在区间[1,e]上恒成立,
即函数f(x)在区间[1,e]上的最大值小于等于1.
因为$f'(x)=\frac{{k(x-\frac{1}{k})(x-1)}}{x^2}$,
令f′(x)=0,得${x_1}=\frac{1}{k},{x_2}=1$.….(9分)
因为0<k<1时,所以$\frac{1}{k}>1$.
当$\frac{1}{k}≥e$时,f'(x)≤0对x∈[1,e]成立,函数f(x)在区间[1,e]上单调递减,….(10分)
所以函数f(x)在区间[1,e]上的最大值为f(1)=k-1<1,
所以不等式f(x)>1在区间[1,e]上无解;….(11分)
当$\frac{1}{k}<e$时,f′(x),f(x)随x的变化情况如下表:
| x | $(1,\frac{1}{k})$ | $\frac{1}{k}$ | $(\frac{1}{k},e)$ |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
此时f(1)=k-1<1,$f(e)=ke-(k+1)-\frac{1}{e}$,
所以$f(e)-1=ke-(k+1)-\frac{1}{e}-1$=$k(e-1)-2-\frac{1}{e}<(e-1)-2-\frac{1}{e}=e-3-\frac{1}{e}<0$.
综上,当0<k<1时,关于x的不等式f(x)>1在区间[1,e]上无解.….(13分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,函数的最值的求法,考查分析问题解决问题的能力.

练习册系列答案
相关题目
7.已知函数f(x)=(x+6)(x-7),g(x)=ax2-(3a+1)x+3,其中a<0,若存在6个整数x0,有f(x0)<0与g(x0)<0同时成立,则a的值可能为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{3}$ | D. | -4 |
16.设全集为R,函数$f(x)=\sqrt{4-{x^2}}$的定义域为M,则∁RM为( )
| A. | [-2,2] | B. | (-2,2) | C. | (-∞,-2]∪[2,+∞) | D. | (-∞,-2)∪(2,+∞) |
17.若一个底面是正三角形且侧棱垂直于底面的三棱柱的正(主)视图如图所示,则其侧面积等于( )


| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
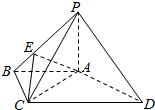 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.