题目内容
已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上为增函数,若f(log2x)>f(1),则x的取值范围是( )
| A、(2,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(0,1)∪(2,+∞) |
考点:对数函数的单调性与特殊点,奇偶性与单调性的综合
专题:函数的性质及应用
分析:由题意根据f(log2x)>f(1),则 log2x>1 ①,或log2x<-1 ②.分别求得①、②的解集,再取并集,即得所求.
解答:
解:∵函数f(x)是定义在R上的偶函数,且在[0,+∞)上为增函数,
若f(log2x)>f(1),则 log2x>1 ①,或log2x<-1 ②.
解①求得x>2,解②求得0<x<
,
故选:C.
若f(log2x)>f(1),则 log2x>1 ①,或log2x<-1 ②.
解①求得x>2,解②求得0<x<
| 1 |
| 2 |
故选:C.
点评:本题主要考查函数的单调性和奇偶性的应用,解对数不等式,体现了转化的数学思想,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
把1010(4)化为十进制数为( )
| A、60 | B、68 | C、70 | D、74 |
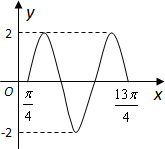 在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=