题目内容
已知函数f（x-1）=4x2，则f（-1）= ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：令x-1=t，得到x=t+1，求出f（t）=4（t+1）2，将x=-1代入即可得到答案．
解答：
解：∵f（x-1）=4x2，
令x-1=t，∴x=t+1，
∴f（t）=4（t+1）2，
∴f（-1）=4（-1+1）2=0，
故答案为：0．
令x-1=t，∴x=t+1，
∴f（t）=4（t+1）2，
∴f（-1）=4（-1+1）2=0，
故答案为：0．
点评：本题考查了求函数的解析式问题，换元法是常用方法之一，本题属于基础题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知函数f（x）是定义在R上的偶函数，且在[0，+∞）上为增函数，若f（log2x）＞f（1），则x的取值范围是（ ）
| A、（2，+∞） | ||
B、（
| ||
C、（0，
| ||
| D、（0，1）∪（2，+∞） |
设a=70.3，b=log70.3，c=0.37，则a，b，c的大小关系是（ ）
| A、a＜b＜c |
| B、b＜c＜a |
| C、c＜a＜b |
| D、c＜b＜a |
函数f（x）=
+lg（x+1）的定义域为（ ）
| 3x2 | ||
|
| A、（-1，1） |
| B、（-1，+∞） |
| C、（1，+∞） |
| D、（-∞，1） |
设全集U=R，集合A={x|x＞1}，B={x|x2-2x-3≥0}，则A∩（∁UB）=（ ）
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1＜x≤1} |
| D、{x|1＜x＜3} |
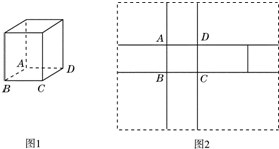图2中的实线围成的部分是长方体（图1）的平面展开图，其中四边形ABCD是边长为1的正方形．若向虚线围成的矩形内任意抛掷一质点，它落在长方体的平面展开图内的概率是已知函数f（x）+1=
，当x∈[0，1]时，f（x）=x．若在区间x∈（-1，1]内，g（x）=f（x）-mx-m有两个零点，则实数m的取值范围是（ ）
| 1 |
| f(x+1) |
A、（0，
| ||
B、[
| ||
C、[0，
| ||
D、[0，
|