题目内容
已知椭圆
+
=1(a>b>0)的离心率为
,F1,F2是其焦点,点P在椭圆上.
(Ⅰ)若∠F1PF2=90°,且△PF1F2的面积等于1,求椭圆的方程;
(Ⅱ)直线PF1交椭圆于另一点Q,分别过点P,Q作直线PQ的垂线,交x轴于点M,N,当|MN|取最小值时,求直线PQ的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)若∠F1PF2=90°,且△PF1F2的面积等于1,求椭圆的方程;
(Ⅱ)直线PF1交椭圆于另一点Q,分别过点P,Q作直线PQ的垂线,交x轴于点M,N,当|MN|取最小值时,求直线PQ的斜率.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)设|PF1|=m,|PF2|=n,由已知可得:
,解得即可;
(II)椭圆
+
=1(a>b>0)的离心率为
,可得
=
,可得椭圆的方程可化为x2+2y2=2c2.
由题意可知PQ的斜率存在,设PQ的方程为:y=k(x+c),P(x1,y1),Q(x2,y2).(k≠0).与椭圆方程联立可得化为(1+2k2)x2+4k2cx+2k2c2-2c2=0,
直线PM的方程为:y-y1=-
(x-x1),令y=0,可得xM=x1+ky1.同理可得xN=x2+ky2,把根与系数的关系代入|MN|=|x2-x1+k(y2-y1)|=|1+k2||x2-x1|=|1+k2|
=
.令t=1+k2>1,f(t)=
,利用导数研究其单调性即可得出.
|
(II)椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
由题意可知PQ的斜率存在,设PQ的方程为:y=k(x+c),P(x1,y1),Q(x2,y2).(k≠0).与椭圆方程联立可得化为(1+2k2)x2+4k2cx+2k2c2-2c2=0,
直线PM的方程为:y-y1=-
| 1 |
| k |
| (x1+x2)2-4x1x2 |
|
| t3 |
| (2t-1)2 |
解答:
解:(I)设|PF1|=m,|PF2|=n,由已知可得:
,解得b2=1,c=1,a2=2.
∴椭圆的标准方程为:
+y2=1.
(II)椭圆
+
=1(a>b>0)的离心率为
,可得
=
,a=
c=
b,
∴椭圆的方程可化为x2+2y2=2c2.
由题意可知PQ的斜率存在,设PQ的方程为:y=k(x+c),P(x1,y1),Q(x2,y2).(k≠0).
联立
,化为(1+2k2)x2+4k2cx+2k2c2-2c2=0,
∴x1+x2=
,x1x2=
,
直线PM的方程为:y-y1=-
(x-x1),令y=0,可得xM=x1+ky1.
同理可得xN=x2+ky2,
∴|MN|=|x2-x1+k(y2-y1)|=|1+k2||x2-x1|=|1+k2|
=2
c
.
令t=1+k2>1,f(t)=
,则f′(t)=
=
.
令f′(t)>0,解得t>
,此时函数f(t)单调递增;令f′(t)<0,解得1<t<
,此时函数f(t)单调递减.
∴当t=
时,函数f(t)取得最小值,f(
)=
,即k2=
时,|MN|取得最小值2
c×
=
.
当k=0时,可得|MN|=2a=2
c.
而2
c>
.
∴当|MN|取最小值时
,直线PQ的斜率k=±
.
|
∴椭圆的标准方程为:
| x2 |
| 2 |
(II)椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
| 2 |
∴椭圆的方程可化为x2+2y2=2c2.
由题意可知PQ的斜率存在,设PQ的方程为:y=k(x+c),P(x1,y1),Q(x2,y2).(k≠0).
联立
|
∴x1+x2=
| -4k2c |
| 1+2k2 |
| 2k2c2-2c2 |
| 1+2k2 |
直线PM的方程为:y-y1=-
| 1 |
| k |
同理可得xN=x2+ky2,
∴|MN|=|x2-x1+k(y2-y1)|=|1+k2||x2-x1|=|1+k2|
| (x1+x2)2-4x1x2 |
| 2 |
|
令t=1+k2>1,f(t)=
| t3 |
| (2t-1)2 |
| 3t2(2t-1)2-t3•4(2t-1) |
| (2t-1)4 |
| t2(2t-3) |
| (2t-1)3 |
令f′(t)>0,解得t>
| 3 |
| 2 |
| 3 |
| 2 |
∴当t=
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 32 |
| 1 |
| 2 |
| 2 |
|
3
| ||
| 2 |
当k=0时,可得|MN|=2a=2
| 2 |
而2
| 2 |
3
| ||
| 2 |
∴当|MN|取最小值时
3
| ||
| 2 |
| ||
| 2 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、相互垂直的直线斜率之间的关系、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
某种放射性元素m克,其衰变函数为y=m•ekx,100年后只剩原来的一半,现有这种元素1克,3年后,剩下( )
| A、0.015g | |||
| B、(1-0.5%)3g | |||
| C、0.925g | |||
D、
|
下列函数中,在区间(0,+∞)上是增函数的是( )
| A、y=-x2 | ||
| B、y=x2-x+2 | ||
C、y=(
| ||
D、y=log0.3
|
 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,∠ABC=90°,PA=PB=3,BC=1,AB=2,AD=3,O是AB的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,∠ABC=90°,PA=PB=3,BC=1,AB=2,AD=3,O是AB的中点.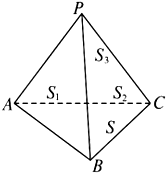 在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为
在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为