题目内容
等差数列{an}的公差为2,且a3=6.
(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)数列{bn}满足bn=
,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)数列{bn}满足bn=
| 1 |
| an |
考点:数列的求和,等差数列的前n项和
专题:计算题,等差数列与等比数列
分析:(Ⅰ)利用等差数列{an}的公差为2,且a3=6,求出a1=2,再求数列{an}的通项公式及前n项和Sn;
(Ⅱ)确定数列{bn}的通项,利用裂项法求数列{bn}的前n项和Tn.
(Ⅱ)确定数列{bn}的通项,利用裂项法求数列{bn}的前n项和Tn.
解答:
解:(Ⅰ)∵等差数列{an}的公差为2,且a3=6,
∴a1=2,
∴an=2+2(n-1)=2n,Sn=2n+
×2=n2+n;
(Ⅱ)bn=
=
-
,
∴Tn=1-
+
-
+…+
-
=1-
=
.
∴a1=2,
∴an=2+2(n-1)=2n,Sn=2n+
| n(n-1) |
| 2 |
(Ⅱ)bn=
| 1 |
| an |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查等差数列的通项与求和,考查裂项法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 根据如图所示的程序据图,回答下列问题:
根据如图所示的程序据图,回答下列问题: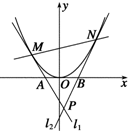 设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若AB=1,求点P的轨迹方程.
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若AB=1,求点P的轨迹方程.