Question

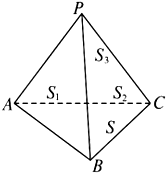在△ABC中，射影定理可以表示为a=bcosC+ccosB，其中a，b，c依次为角A、B、C的对边．类比以上定理，如图，在四面体P-ABC中，S₁、S₂、S₃、S分别表示△PAB、△PBC、△PCA、△ABC的面积，α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小，我们猜想将射影定理类比推广到三维空间，其表现形式应为

 

．

Answer 1

考点：类比推理

专题：综合题,推理和证明

分析：这是一个类比推理的题，在由平面图形到空间图形的类比推理中，一般是由点的性质类比推理到线的性质，由线的性质类比推理到面的性质，即可得出结论．

解答： 解：由已知在平面几何中，在△ABC中，如果点A在BC边上的射影是D，△ABC的三边BC、AC、AB的长依次是a、b、c，则a=b•cosC+c•cosb，
我们可以类比这一性质，推理出：
若四面体P-ABC中，△ABC、△PAB、△PBC、△PCA的面积依次为S、S₁、S₂、S₃，
二面角P-AB-C、P-BC-A、P-CA-B的度数依次为α、β、γ，则S=S₁cosα+S₂cosβ+S₃cosγ．
故答案为：S=S₁cosα+S₂cosβ+S₃cosγ．

点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．