题目内容
已知f(x)=
sin2x+cos2x-
(1)求函数f(x)的最小正周期及单调递增区间.
(2)当x∈[0,
]时,方程f(x)-m=0有实数解,求实数m的取值范围.
| ||
| 2 |
| 3 |
| 2 |
(1)求函数f(x)的最小正周期及单调递增区间.
(2)当x∈[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:(1)先化简求得解析式f(x)=sin(2x+
)-1,根据正弦函数的图象和性质即可求得函数f(x)的最小正周期及单调递增区间.
(2)先求得2x+
∈[
,
],从而可得f(x)∈[-
,0],由f(x)=m,即可求得实数m的取值范围.
| π |
| 6 |
(2)先求得2x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 3 |
| 2 |
解答:
解:(1)∵f(x)=
sin2x+
-
=
sin2x+
cos2x-1=sin(2x+
)-1
∴f(x)=sin(2x+
)-1…(2分)
∴最小正周期为π…(4分)
令∴z=2x+
.函数f(x)=sinz-1的单调递增区间是[-
+2kπ,
+2kπ],k∈Z,
由-
+2kπ≤2x+
≤
+2kπ,
得-
+kπ≤x≤
+kπ,k∈Z,
∴函数f(x)的单调递增区间是[-
+kπ,
+kπ],k∈Z…(6分)
(2)当x∈[0,
]时,2x+
∈[
,
],
sin(2x+
)∈[-
,1],
f(x)∈[-
,0],
∵f(x)=m,
∴m∈[-
,0]…(12分).
| ||
| 2 |
| 1+cos2x |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴f(x)=sin(2x+
| π |
| 6 |
∴最小正周期为π…(4分)
令∴z=2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得-
| π |
| 3 |
| π |
| 6 |
∴函数f(x)的单调递增区间是[-
| π |
| 3 |
| π |
| 6 |
(2)当x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
sin(2x+
| π |
| 6 |
| 1 |
| 2 |
f(x)∈[-
| 3 |
| 2 |
∵f(x)=m,
∴m∈[-
| 3 |
| 2 |
点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象与性质,属于基础题.

练习册系列答案
相关题目
函数f(x)=
的值域是( )
|
| A、[-4,+∞) |
| B、[0,+∞) |
| C、[4,+∞) |
| D、(-∞,+∞) |
“x2-x-2<0”是“|x|<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
 函数f(x)=cos(πx+φ)(0<φ<
函数f(x)=cos(πx+φ)(0<φ<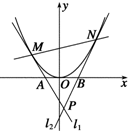 设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若AB=1,求点P的轨迹方程.
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若AB=1,求点P的轨迹方程.