题目内容
9.已知函数f(x)=x2+bx过(1,3)点,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则Sn的值为( )| A. | $\frac{n+1}{n+2}$ | B. | $\frac{n+1}{2n+4}$ | C. | $\frac{3}{2}$-$\frac{2n+3}{(n+1)(n+2)}$ | D. | $\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$ |
分析 利用数列与函数的关系求出b,得到数列的通项公式,然后利用裂项法求解数列的和即可.
解答 解:函数f(x)=x2+bx过(1,3)点,
可得:3=1+b,解得b=2,
可知:f(n)=n(n+2),∴$\frac{1}{f(n)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴Sn=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n-1}-\frac{1}{n+1}+\frac{1}{n}-\frac{1}{n+2})$
=$\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$.
故选:D.
点评 本题考查数列与函数相结合,数列的通项公式以及数列求和,考查转化思想以及计算能力.

练习册系列答案
相关题目
19.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )
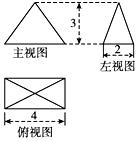

| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 4$\sqrt{10}$+2$\sqrt{13}$ | D. | 2$\sqrt{10}$+$\sqrt{13}$ |
20.已知a、b∈{2,3,4,5,6,7,8,9},则logab的不同取值个数为( )
| A. | 53 | B. | 56 | C. | 55 | D. | 57 |
17.在方程|x|+|y|=1表示的曲线所围成的区域内(包含边界)任取一点P(x,y),则z=xy的最大值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
4.集合A={x∈N|x2-4x-5<0},B={x|log2(x-2)≤1},则A∩B=( )
| A. | (-1,4] | B. | (2,4] | C. | (3,4) | D. | {3,4} |
18.已知函数f(x)=$\left\{\begin{array}{l}{lg(x+m),0<x<1}\\{\sqrt{x},x≥1}\end{array}\right.$在(0,+∞)上是增函数,则实数m的取值范围是( )
| A. | (-∞,9] | B. | (0,9] | C. | [0,9] | D. | [0,9) |