题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{lg(x+m),0<x<1}\\{\sqrt{x},x≥1}\end{array}\right.$在(0,+∞)上是增函数,则实数m的取值范围是( )| A. | (-∞,9] | B. | (0,9] | C. | [0,9] | D. | [0,9) |
分析 利用分段函数的单调性以及函数的端点的函数值的关系,转化求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{lg(x+m),0<x<1}\\{\sqrt{x},x≥1}\end{array}\right.$在(0,+∞)上是增函数,
可知x≥1时,函数是增函数,
0<x<1时,y=lg(x+m)是增函数,并且lg(1+m)≤1,
解得0≤m≤9.
故选:C.
点评 本题考查分段函数的单调性的判断与应用,注意端点值的判断,是易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知函数f(x)=x2+bx过(1,3)点,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则Sn的值为( )
| A. | $\frac{n+1}{n+2}$ | B. | $\frac{n+1}{2n+4}$ | C. | $\frac{3}{2}$-$\frac{2n+3}{(n+1)(n+2)}$ | D. | $\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$ |
6.实数x,y满足$\left\{\begin{array}{l}x-2y+2≥0\\ x+y≤1\\ y+1≥0\end{array}\right.$且z=2x-y,则z的最大值为( )
| A. | -7 | B. | -1 | C. | 5 | D. | 7 |
13. 中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
(1)由以上统计数据填2×2列联表,并判断是否95%的把握认为以45岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动,现从这8人中随机抽2人.
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率;
②记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
| 45岁以下 | 45岁以上 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率;
②记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
8.已知$f(x)=\frac{e^x}{{{x^2}+a}}({a>0})$的两个极值点分别为x1,x2(x1<x2),则ax2取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | $({1,\frac{32}{27}}]$ | D. | $({0,\frac{32}{27}}]$ |
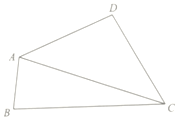 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2, 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2