题目内容
设集合P={x|
≤0},Q={x||x-
|≤
},那么“m∈P”是“m∈Q”的( )
| x |
| x-1 |
| 3 |
| 2 |
| 3 |
| 2 |
| A、充分不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:解分式不等式和绝对值不等式,求出集合P和信Q,进而根据两个集合的包含关系,进而可用集合法判断出“m∈P”与“m∈Q”的充要关系.
解答:
解:由
≤0得:0≤x<1,
故集合P={x|
≤0}=[0,1),
解|x-
|≤
,得0≤x≤3,
故集合Q={x||x-
|≤
}=[0,3],
∵P?Q,
故“m∈P”是“m∈Q”的充分不必要条件;
故选:A.
| x |
| x-1 |
故集合P={x|
| x |
| x-1 |
解|x-
| 3 |
| 2 |
| 3 |
| 2 |
故集合Q={x||x-
| 3 |
| 2 |
| 3 |
| 2 |
∵P?Q,
故“m∈P”是“m∈Q”的充分不必要条件;
故选:A.
点评:判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
已知x,y的取值如下表,从所得的散点图分析,y与x线性相关,则
=1.1x+
,则
=( )
 |
| y |
 |
| a |
 |
| a |
| x | 0 | 1 | 3 | 4 |
| y | 1 | 2 | 3 | 6 |
| A、-0.4 | B、0.8 |
| C、-1 | D、-1.2 |
复数
的虚部是( )
| i2014 |
| 1-2i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
设全集U是实数集R,M={x||2x-3|≥4},N={x|log
(x+2)≥0},则M∩N=( )
| 1 |
| 3 |
A、{x|x≤-
| ||
B、{x|-2<x≤-
| ||
C、{x|-
| ||
| D、{x|-2<x≤-1} |
二项式(x-1)n的奇数项二项式系数和64,若(x-1)n=a0+a1(x+1)+a2(x+1)2+…+an(x+1)n,则a1等于( )
| A、-14 | B、448 |
| C、-1024 | D、-16 |
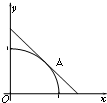 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的最大值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的最大值为( )