题目内容
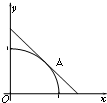 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的最大值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的最大值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意,若点B落在区域M内的概率为P,P取最大,则过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N的面积最小,即直角三角形斜边长最小.
解答:
解:由题意,若点B落在区域M内的概率为P,P取最大,
则过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N的面积最小,即直角三角形斜边长最小.
设∠AOx=α,则直角三角形斜边长为tanα+
≥2,
当且仅当α=45°时,直角三角形斜边长最小直角三角形斜边长最小,此时三角形的面积为1,
∴P的最大值为
=
.
故选:D.
则过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N的面积最小,即直角三角形斜边长最小.
设∠AOx=α,则直角三角形斜边长为tanα+
| 1 |
| tanα |
当且仅当α=45°时,直角三角形斜边长最小直角三角形斜边长最小,此时三角形的面积为1,
∴P的最大值为
| ||
| 1 |
| π |
| 4 |
故选:D.
点评:本题考查几何概型,考查学生分析解决问题的能力,确定直角三角形斜边长最小是关键.

练习册系列答案
相关题目
设集合P={x|
≤0},Q={x||x-
|≤
},那么“m∈P”是“m∈Q”的( )
| x |
| x-1 |
| 3 |
| 2 |
| 3 |
| 2 |
| A、充分不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知全集U=R,集合A={y|y≥0},集合B={x|1≤x≤3},则如图所示的阴影部分表示的集合是( )


| A、{x|0≤x<1,或x>3} |
| B、{x|0≤x<1} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
已知函数 f(x)=ax3+f′(2)x2+3,若 f′(1)=-5,则f′(2)=( )
| A、-l | B、-2 | C、-3 | D、-4 |
已知曲线y=cosx,其中x∈[0,
π],则该曲线与坐标轴围成的面积等于( )
| 3 |
| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
在复平面内,复数
对应的点位于( )
| -3+i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
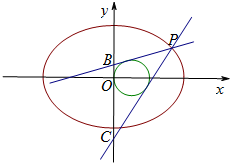 设椭圆E:
设椭圆E: