题目内容
甲组有6人,乙组有4人,其中组长各1人.
(Ⅰ)这10人站成一排照相,根据下列要求,各有多少种排法?
①同组人员相邻;
②乙组人员不相邻.
(Ⅱ)现选派5人去参加比赛,根据下列要求,各有多少种选派方法?
①甲组3人,乙组2人;
②组长中至少有1人参加.
(Ⅰ)这10人站成一排照相,根据下列要求,各有多少种排法?
①同组人员相邻;
②乙组人员不相邻.
(Ⅱ)现选派5人去参加比赛,根据下列要求,各有多少种选派方法?
①甲组3人,乙组2人;
②组长中至少有1人参加.
考点:计数原理的应用
专题:排列组合
分析:(Ⅰ)①利用捆绑法,把同组的捆绑在一起,先在组内排列,再两组排,
②利用插空法,先排甲组有7个空,任选4个排列,问题得以解决.
(Ⅱ)①利用分步计数原理,根据组合定义,选择即可,
②利用分类计数原理,分组长有1人参加,两个组长都参加,问题得以解决.
②利用插空法,先排甲组有7个空,任选4个排列,问题得以解决.
(Ⅱ)①利用分步计数原理,根据组合定义,选择即可,
②利用分类计数原理,分组长有1人参加,两个组长都参加,问题得以解决.
解答:
解:(Ⅰ)①
•
•
=720×24×2=34560;
②
•
=720×840=604800.
(Ⅱ)①
•
=20×6=120;
②
•
+
•
=140+56=196.
| A | 6 6 |
| A | 4 4 |
| A | 2 2 |
②
| A | 6 6 |
| A | 4 7 |
(Ⅱ)①
| C | 3 6 |
| C | 2 4 |
②
| C | 1 2 |
| C | 4 8 |
| C | 2 2 |
| C | 3 8 |
点评:本题主要考查了排列中的捆绑法和插空法,关键是特殊元素优先安排,属于基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
设集合P={x|
≤0},Q={x||x-
|≤
},那么“m∈P”是“m∈Q”的( )
| x |
| x-1 |
| 3 |
| 2 |
| 3 |
| 2 |
| A、充分不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在复平面内,复数
对应的点位于( )
| -3+i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
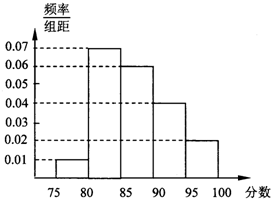 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: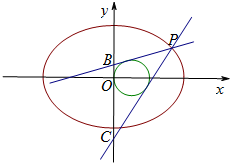 设椭圆E:
设椭圆E: