题目内容
二项式(x-1)n的奇数项二项式系数和64,若(x-1)n=a0+a1(x+1)+a2(x+1)2+…+an(x+1)n,则a1等于( )
| A、-14 | B、448 |
| C、-1024 | D、-16 |
考点:二项式定理的应用
专题:综合题,二项式定理
分析:利用二项式(x-1)n的奇数项二项式系数和64,求出n,再求出a1的值.
解答:
解:∵二项式(x-1)n的奇数项二项式系数和64,
∴2n-1=64,
∴n=7,
由已知(x-1)7=[(x+1)-2]7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7,
故a1=
•(-2)6=448.
故选:B.
∴2n-1=64,
∴n=7,
由已知(x-1)7=[(x+1)-2]7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7,
故a1=
| C | 1 7 |
故选:B.
点评:本题考查二项式系数的性质,考查展开式中的指定项,确定n的值是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
设集合P={x|
≤0},Q={x||x-
|≤
},那么“m∈P”是“m∈Q”的( )
| x |
| x-1 |
| 3 |
| 2 |
| 3 |
| 2 |
| A、充分不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若平面内两个向量
=(2cosθ,1)与
=(1,cosθ)共线,则cos2θ等于( )
| a |
| b |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
已知全集U=R,集合A={y|y≥0},集合B={x|1≤x≤3},则如图所示的阴影部分表示的集合是( )


| A、{x|0≤x<1,或x>3} |
| B、{x|0≤x<1} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
已知函数 f(x)=ax3+f′(2)x2+3,若 f′(1)=-5,则f′(2)=( )
| A、-l | B、-2 | C、-3 | D、-4 |
在复平面内,复数
对应的点位于( )
| -3+i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

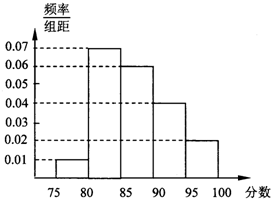 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: