题目内容
定义在(-2,2)的奇函数f(x),满足f(1+a)+f(a)>0,又当x≥0时,f(x)是减函数,求a的取值范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用奇函数定义把不等式f(1+a)+f(a)>0转化f(1+a)>f(-a),
再利用函数的单调性,和定义域转为关于a的不等式组求解.
再利用函数的单调性,和定义域转为关于a的不等式组求解.
解答:
解:∵函数f(x)为奇函数,且当x≥0时,f(x)是减函数
∴f(x)在R上是减函数
∴f(1+a)+f(a)>0,得f(1+a)>-f(a)=f(-a)
f(1+a)>f(-a)
即-a>1+a,∴a<-
∵定义在(-2,2)上
∴-2<1+a<2且-2<a<2
解上述不等式可得:-2<a<-
所以a的取值范围:(-2,-
)
∴f(x)在R上是减函数
∴f(1+a)+f(a)>0,得f(1+a)>-f(a)=f(-a)
f(1+a)>f(-a)
即-a>1+a,∴a<-
| 1 |
| 2 |
∵定义在(-2,2)上
∴-2<1+a<2且-2<a<2
解上述不等式可得:-2<a<-
| 1 |
| 2 |
所以a的取值范围:(-2,-
| 1 |
| 2 |
点评:本题考察了函数的奇偶性,和单调性,转化为不等式解决,注意函数的定义域对变量的限制.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
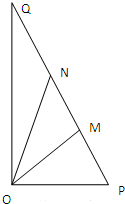 某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40
某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40