题目内容
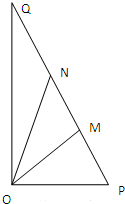 某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40
某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40| 3 |
考点:解三角形的实际应用
专题:解三角形
分析:由已知得∠OPQ=60°,从而∠PQO=30°,设∠POM=α,0°≤α≤60°,由正弦定理可得OM=
,ON=
,故S△OMN=
OM•ONsin∠MON=
,由此能求出∠POM=15°时,△OMN的面积最小,面积的最小值1200(2-
).
| OPsin60° |
| sin(60°+α) |
| OPsin60° |
| sin(90°+α) |
| 1 |
| 2 |
| 1200 | ||
2sin(2α+60°)+
|
| 3 |
解答:
解:∵Rt△OPQ中,∠POQ=90°,OP=40m,OQ=40
m,
∴tan∠OPQ=
=
=
,
∴∠OPQ=60°,∴∠PQO=30°,
设∠POM=α,0°≤α≤60°,
在△OMP中,由正弦定理可得:
=
,
OM=
,
同理,ON=
,
故S△OMN=
OM•ONsin∠MON
=
×
=
=
=
因为0°≤α≤60°,所以60°≤2α+60°≤180°,
所以当α=15°,即∠POM=15°时,sin(2α+60°)的最大值为1,
此时,△OMN的面积最小,面积的最小值1200(2-
).
| 3 |
∴tan∠OPQ=
| OQ |
| PO |
40
| ||
| 40 |
| 3 |
∴∠OPQ=60°,∴∠PQO=30°,
设∠POM=α,0°≤α≤60°,
在△OMP中,由正弦定理可得:
| OM |
| sin∠OPM |
| OP |
| sin∠OMP |
OM=
| OPsin60° |
| sin(60°+α) |
同理,ON=
| OPsin60° |
| sin(90°+α) |
故S△OMN=
| 1 |
| 2 |
=
| 1 |
| 4 |
| OP2•sin260° |
| sin(60°+α)sin(90°+α) |
=
| 600 | ||
|
=
| 600 | ||||||||||
|
=
| 1200 | ||
2sin(2α+60°)+
|
因为0°≤α≤60°,所以60°≤2α+60°≤180°,
所以当α=15°,即∠POM=15°时,sin(2α+60°)的最大值为1,
此时,△OMN的面积最小,面积的最小值1200(2-
| 3 |
点评:本题考查当∠POM取何值时,人工湖的面积最小,并求面积的最小值,解题时要认真审题,注意正弦定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果sinα=
,那么sin(π+α)=( )
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
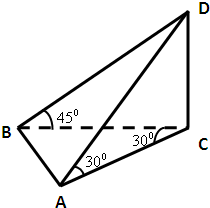 如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔
如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔