题目内容
曲线f(x)=cosx(x>0)上所有切线斜率为0的切点按从左至右的顺序排成点列(an,f(an))(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=
,数列{bn}的前n项和为Tn,求cosT6的值.
(1)求数列{an}的通项公式;
(2)设bn=
| an |
| 2n |
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(1)利用导数运算的法则可得f′(x)=-sinx,令f′(x)=0,解得x=kπ(k∈N*),利用等差数列的通项公式即可得出;
(2)bn=
=
,再利用“错位相减法”可得Tn=π(2-
).再利用诱导公式即可得出cosT6.
(2)bn=
| an |
| 2n |
| nπ |
| 2n |
| 2+n |
| 2n |
解答:
解:(1)∵f(x)=cosx(x>0),∴f′(x)=-sinx,
令f′(x)=0,解得x=kπ(k∈N*),
∴数列{an}是以π为首项,π为公差的等差数列,
∴an=π+(n-1)π=nπ(n∈N*).
(2)bn=
=
,
∴Tn=π(
+
+
+…+
),
Tn=π(
+
+…+
+
),
两式相减可得:
Tn=π(
+
+…+
-
)
=π[
-
]
=π(1-
-
),
∴Tn=π(2-
).
∴cosT6=cosπ(2-
)=cos
=
=
.
令f′(x)=0,解得x=kπ(k∈N*),
∴数列{an}是以π为首项,π为公差的等差数列,
∴an=π+(n-1)π=nπ(n∈N*).
(2)bn=
| an |
| 2n |
| nπ |
| 2n |
∴Tn=π(
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n-1 |
| 2n |
| n |
| 2n+1 |
两式相减可得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
=π[
| ||||
1-
|
| n |
| 2n+1 |
=π(1-
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=π(2-
| 2+n |
| 2n |
∴cosT6=cosπ(2-
| 8 |
| 26 |
| π |
| 8 |
|
| ||||
| 2 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”、诱导公式即可得出,考查了推理能力与计算能力,属于难题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
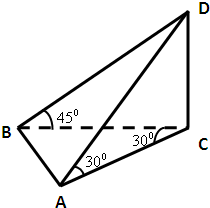 如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔
如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔