题目内容
不等式|4-x2|+
≥0的解集是( )
| |x| |
| x |
A、{x|x≤-
| ||||
| B、{x|x>0} | ||||
C、{x|x≤-
| ||||
D、{x|x≤-
|
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:分别讨论:①x∈(-∞,-2]时②x∈(-2,0)时③x∈(-2,0)时④x∈[2,+∞)时的情况,解不等式,从而求出不等式的解集.
解答:
解:①x∈(-∞,-2]时,|4-x2|+
=x2-4-1≥0,解得:x≤-
,
②x∈(-2,0)时,|4-x2|+
=4-x2-1≥0,解得:-
≤x<0,
③x∈(-2,0)时,|4-x2|+
=4-x2+1≥0,解得:0<x<2,
④x∈[2,+∞)时,|4-x2|+
=x2-4+1≥0,解得:x≥
,
综上:不等式|4-x2|+
≥0的解集是:{x|x≤-
,或-
≤x<0或x>0}.
| |x| |
| x |
| 5 |
②x∈(-2,0)时,|4-x2|+
| |x| |
| x |
| 3 |
③x∈(-2,0)时,|4-x2|+
| |x| |
| x |
④x∈[2,+∞)时,|4-x2|+
| |x| |
| x |
| 3 |
综上:不等式|4-x2|+
| |x| |
| x |
| 5 |
| 3 |
点评:本题考查了绝对值不等式的解法,考查分类讨论思想,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,若AB=4,BC=2
,且
•
=-8,则AC等于( )
| 2 |
| BA |
| BC |
A、4
| ||
| B、4 | ||
C、2
| ||
D、2
|
P是椭圆
+
=1上一点,F1,F2分别为左、右焦点,△PF1F2的内切圆的半径为1,则|
+
|的值为( )
| x2 |
| 25 |
| y2 |
| 9 |
| PF1 |
| PF2 |
| A、8 | ||||
B、4
| ||||
| C、4 | ||||
D、
|
 如图,矩形ABCD,点A,B分别在x正半轴和y正半轴上,点C,D在第一象限内|
如图,矩形ABCD,点A,B分别在x正半轴和y正半轴上,点C,D在第一象限内|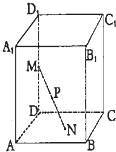 已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )
已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )