题目内容
试就实数k的取值,讨论|x2-2x-3|=k的解的个数.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:先画出函数y=|x2-2x-3|及y=k的图象,利用图象容易是问题获得解答.
解答:
解:先做出函数y=x2-2x-3的图象,易知y=(x-1)2-4
然后保留其x轴上方的图象,再将x轴下方的图象沿x轴对称上来,即可得到y=|x2-2x-3|的图象,
则原方程根的个数即为y=|x2-2x-3|的图象与y=k图象交点的个数.
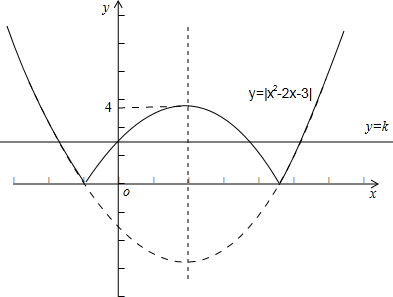
如图:
(1)当k<0时,直线y=k与函数y=|x2-2x-3|无交点,故原方程无根;
(2)当k=0或k>4时,直线y=k与函数y=|x2-2x-3|有两个交点,故原方程有两个实数根;
(3)当k=4时,直线y=k与函数y=|x2-2x-3|有三个交点,故原方程有三个实数根;
(4)当0<k<4时,直线y=k与函数y=|x2-2x-3|有四个交点,故原方程有四个实数根.
然后保留其x轴上方的图象,再将x轴下方的图象沿x轴对称上来,即可得到y=|x2-2x-3|的图象,
则原方程根的个数即为y=|x2-2x-3|的图象与y=k图象交点的个数.
如图:
(1)当k<0时,直线y=k与函数y=|x2-2x-3|无交点,故原方程无根;
(2)当k=0或k>4时,直线y=k与函数y=|x2-2x-3|有两个交点,故原方程有两个实数根;
(3)当k=4时,直线y=k与函数y=|x2-2x-3|有三个交点,故原方程有三个实数根;
(4)当0<k<4时,直线y=k与函数y=|x2-2x-3|有四个交点,故原方程有四个实数根.

点评:此题考查了方程的根、函数的零点之间的关系,一般采用数形结合的思想方法解决.

练习册系列答案
相关题目
过双曲线2x2-y2-2=0的右焦点作直线l交曲线于A、B两点,若|AB|=4则这样的直线存在( )
| A、0条 | B、1条 | C、2条 | D、3条 |
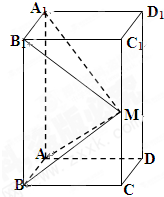 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点