题目内容
过双曲线x2-
=1的左顶点A作斜率为1的直线l,若l与该双曲线的其中一条渐近线相交于点(
,y0),则该双曲线的离心率是 .
| y2 |
| b2 |
| 1 |
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出A(1,0),l的方程y=x-1,渐近线为:y=±bx,l与该双曲线的其中一条渐近线相交于点(
,y0),在求出b的值,即可求离心率.
| 1 |
| 2 |
解答:
解:∵双曲线x2-
=1的左顶点A(1,0),
∴斜率为1的直线l的方程为:y=x-1,渐近线为:y=±bx,
∵l与该双曲线的其中一条渐近线相交于点(
,y0),
∴点为(
,-
),-
b=-
,b=1,
可得:双曲线的方程为x2-y2=1,
所以该双曲线的离心率是
,
故答案为:
,
| y2 |
| b2 |
∴斜率为1的直线l的方程为:y=x-1,渐近线为:y=±bx,
∵l与该双曲线的其中一条渐近线相交于点(
| 1 |
| 2 |
∴点为(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
可得:双曲线的方程为x2-y2=1,
所以该双曲线的离心率是
| 2 |
故答案为:
| 2 |
点评:本题考查了双曲线的简单几何性质,应用直线方程解决问题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
在直二面角α-l-β的棱l上取一点A、过A分别在α,β内A的同侧作与l成45°的直线,则这两条直线所夹的角为( )
| A、45° | B、60° |
| C、90° | D、120° |
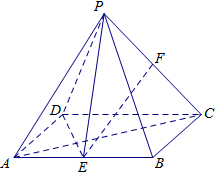 如图,四棱锥P-ABCD的底面为矩形,AB=
如图,四棱锥P-ABCD的底面为矩形,AB=