Question

已知函数f（x）=

1-(1-x)2 ，(0≤x＜2) f(x-2)，(x≥2)

，若关于x的方程f（x）=kx（k＞0）有且只有四个不相等的实数根，则实数k的取值范围是

 

．

Answer 1

考点：函数的零点与方程根的关系

专题：计算题,作图题,函数的性质及应用

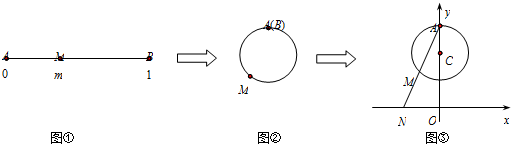
分析：令g（x）=kx（k＞0），将方程的解的个数化为函数交点的个数，作出函数f（x）=

1-(1-x)2 ，(0≤x＜2) f(x-2)，(x≥2)

 的图象，从图象中得到实数k的取值范围．

解答： 解：令g（x）=kx（k＞0），
则方程f（x）=kx（k＞0）有且只有四个不相等的实数根可转化为
函数f（x）与g（x）有且只有四个交点；
作出函数f（x）=

1-(1-x)2 ，(0≤x＜2) f(x-2)，(x≥2)

 的图象如下图，

当与第二半圆相切时，有3个交点，此时，k=

1

32-1

=

2

4

，
当与第三半圆相切时，有5个交点，此时，k=

1

52-1

=

6

12

，
则实数k的取值范围为（

6

12

，

2

4

）．
故答案为：（

6

12

，

2

4

）．

点评：本题考查了方程的解与函数的零点之间的关系，同时考查了学生的作图能力及数形结合的思想，属于中档题．