题目内容
某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )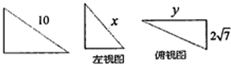

A、2
| ||
B、4
| ||
C、8
| ||
D、16
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:首先,根据三视图,得到该几何体的具体的结构特征,然后,建立关系式:
=
,然后,求解当xy最大时,该几何体的具体的结构,从而求解其体积.
x2-(2
|
| 102-y2 |
解答:
解:由三视图,得
该几何体为三棱锥,
有
=
,
∴x2+y2=128,
∵xy≤
=64,当且仅当x=y=8时,等号成立,
此时,V=
×
×2
×6×8=16
,
故选:D.
该几何体为三棱锥,
有
x2-(2
|
| 102-y2 |
∴x2+y2=128,
∵xy≤
| x2+y2 |
| 2 |
此时,V=
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 7 |
故选:D.
点评:本题重点考查了三视图、几何体的体积计算等知识,属于中档题.

练习册系列答案
相关题目
椭圆的焦点为F1,F2,过F1的最短弦PQ的长为10,△PF2Q的周长为36,则此椭圆的离心率为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,已知tanA•tanB>1,则△ABC是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、最小内角大于45°的三角形 |
已知x,y之间的数据如表所示,则回归直线过点( )
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1.2 | 1.8 | 2.5 | 3.2 | 3.8 |
| A、(0,0) |
| B、(2,1.8) |
| C、(3,2.5) |
| D、(4,3.2) |
下列函数中,在(0,+∞)上是减函数的是( )
A、y=
| |||||
| B、y=x2 | |||||
| C、y=2x | |||||
D、y=
|
若直线y=ax+3与直线y=-2x-6垂直,则实数a的值为( )
| A、-2 | ||
B、
| ||
C、-
| ||
| D、2 |