题目内容
若直线y=ax+3与直线y=-2x-6垂直，则实数a的值为（ ）
| A、-2 | ||
B、
| ||
C、-
| ||
| D、2 |
考点：直线的一般式方程与直线的性质
专题：直线与圆
分析：利用直线与直线垂直的性质求解．
解答：
解：∵直线y=ax+3与直线y=-2x-6垂直，
∴-2a+1=0，解得a=
．
∴实数a的值为
．
故选：B．
∴-2a+1=0，解得a=
| 1 |
| 2 |
∴实数a的值为
| 1 |
| 2 |
故选：B．
点评：本题考查实数值的求法，是基础题，解题时要认真审题，注意直线与直线垂直的条件的灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知a、b∈R，a+bi是虚数的充分必要条件是（ ）
| A、ab≠0 | B、a≠0 |
| C、b≠0 | D、a=0且b≠0 |
设a∈R，若函数y=ex+3ax，x∈R有大于零的极值点，则（ ）
| A、a＞-3 | ||
| B、a＜-3 | ||
C、a＞-
| ||
D、a＜-
|
某几何体的三视图如图所示，当xy最大时，该几何体的体积为（ ）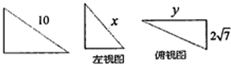
A、2
| ||
B、4
| ||
C、8
| ||
D、16
|
已知cosα=-
，sinα=
，那么α的终边所在的象限为（ ）
| 3 |
| 5 |
| 4 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
“-3＜m＜-1”是方程
+
=1表示双曲线的（ ）
| x2 |
| 2+m |
| y2 |
| m+1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |