题目内容
已知函数f(x)=x2-lnx.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调增区间.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调增区间.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:计算题,导数的概念及应用
分析:(1)求导数,并求切点,应用点斜式方程求出切线方程;(2)令f′(x)>0,解不等式,求出单调增区间,注意函数的定义域.
解答:
解:(1)依题意,函数f(x)的定义域为(0,+∞),
f′(x)=2x-
,f(1)=1,f′(1)=2-1=1,
故曲线y=f(x)在点(1,f(1))处的切线方程为:y-1=x-1即y=x;
(2)依题意,函数f(x)的定义域为(0,+∞),
f′(x)=2x-
,
令f′(x)>0,解得,x>
或x<-
,
故函数f(x)的单调增区间为(
,+∞).
f′(x)=2x-
| 1 |
| x |
故曲线y=f(x)在点(1,f(1))处的切线方程为:y-1=x-1即y=x;
(2)依题意,函数f(x)的定义域为(0,+∞),
f′(x)=2x-
| 1 |
| x |
令f′(x)>0,解得,x>
| ||
| 2 |
| ||
| 2 |
故函数f(x)的单调增区间为(
| ||
| 2 |
点评:本题主要考查导数的几何意义,考查应用导数求切线方程,考查应用导数求单调区间,是一道基础题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )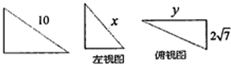

A、2
| ||
B、4
| ||
C、8
| ||
D、16
|
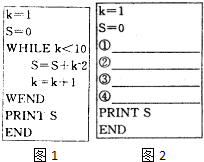 图1给出一个用“当型”循环语句编写的程序:
图1给出一个用“当型”循环语句编写的程序: 在2014年清明节期间,高速公路车辆较多,某调查公司在服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取40名驾驶员进行调查,将他们在某段高速公路上的车速(km/h)分成6段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如图的频率分布直方图.
在2014年清明节期间,高速公路车辆较多,某调查公司在服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取40名驾驶员进行调查,将他们在某段高速公路上的车速(km/h)分成6段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如图的频率分布直方图.