题目内容
椭圆的焦点为F1,F2,过F1的最短弦PQ的长为10,△PF2Q的周长为36,则此椭圆的离心率为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据三角形的周长求出a的值,再根据勾股定理求出c的值,最后根据离心率公式计算即可.
解答:
解:设椭圆方程为
+
=1,
∵△PF2Q的周长为36,
∴PF2+QF2+PQ=36=4a,
解得a=9,
∵过F1的最短弦PQ的长为10
∴PF2=QF2=
(36-10)=13,
在直角三角形QF1F2中,根据勾股定理得,
2C=
=
=12,
∴c=6,
∴e=
=
=
故选:C.
| x2 |
| a2 |
| y2 |
| b2 |
∵△PF2Q的周长为36,
∴PF2+QF2+PQ=36=4a,
解得a=9,
∵过F1的最短弦PQ的长为10
∴PF2=QF2=
| 1 |
| 2 |
在直角三角形QF1F2中,根据勾股定理得,
2C=
| QF22-QF12 |
| 132-52 |
∴c=6,
∴e=
| c |
| a |
| 6 |
| 9 |
| 2 |
| 3 |
故选:C.
点评:本题考查了椭圆方程的定义和离心率的计算,属于基础题.

练习册系列答案
相关题目
已知a、b∈R,a+bi是虚数的充分必要条件是( )
| A、ab≠0 | B、a≠0 |
| C、b≠0 | D、a=0且b≠0 |
已知tanα=-
,sinβ=
,β∈(
,π),则tan(2α-β)=( )
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
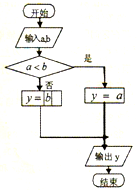 定义某种运算※,a※b的运算原理如图所示,设f(x)=(0※x)x-(2※x),则f(x)在区间[-2,2]上的最小值为( )
定义某种运算※,a※b的运算原理如图所示,设f(x)=(0※x)x-(2※x),则f(x)在区间[-2,2]上的最小值为( )| A、-2 | B、-4 | C、-6 | D、0 |
已知a=log1.20.3,b=log1.20.8,c=1.50.5,则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
设a∈R,若函数y=ex+3ax,x∈R有大于零的极值点,则( )
| A、a>-3 | ||
| B、a<-3 | ||
C、a>-
| ||
D、a<-
|
某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )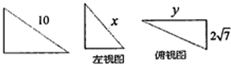

A、2
| ||
B、4
| ||
C、8
| ||
D、16
|