题目内容
下列函数中,在(0,+∞)上是减函数的是( )
A、y=
| |||||
| B、y=x2 | |||||
| C、y=2x | |||||
D、y=
|
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据反比例函数,二次函数,指数函数和一次函数的图象和性质,逐一分析四个答案中函数在(0,+∞)上的单调性,从而可得答案.
解答:
解:y=
在区间(0,+∞)上是减函数;
y=x2在区间(0,+∞)上是增函数,故排除B;
y=2x区间(0,+∞)上是增函数,故排除C;
y=
在区间(0,+∞)上可化为:y=x是增函数,可排除D,
故选:A.
| 1 |
| x |
y=x2在区间(0,+∞)上是增函数,故排除B;
y=2x区间(0,+∞)上是增函数,故排除C;
y=
|
故选:A.
点评:本题考查函数的单调性的判断,属基础题.判断函数的单调性可利用定义、图象等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a=log1.20.3,b=log1.20.8,c=1.50.5,则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
已知数列{an}满足的前n项和Sn=n2+n+1,那么它的通项公式为an=( )
| A、an=n+1 | |||||
B、an=
| |||||
| C、an=2n | |||||
D、an=
|
某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )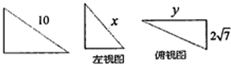

A、2
| ||
B、4
| ||
C、8
| ||
D、16
|
在数学拓展课上,老师定义了一种运算“*”:对于n∈N,满足以下运算性质:①2*2=1;②(2n+2)*2=(2n*2)+3.则1020*2的数值为( )
| A、1532 | B、1533 |
| C、1528 | D、1536 |
“-3<m<-1”是方程
+
=1表示双曲线的( )
| x2 |
| 2+m |
| y2 |
| m+1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
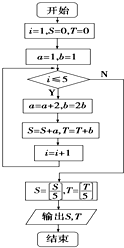 阅读程序框图设[x]表示取x的整数部分,如[5]=5,[2.7]=2,经过程序框图运行后输出结果为S,T,设z1=S-Ti,z2=1+i,z=z1•z2,则|z|=
阅读程序框图设[x]表示取x的整数部分,如[5]=5,[2.7]=2,经过程序框图运行后输出结果为S,T,设z1=S-Ti,z2=1+i,z=z1•z2,则|z|=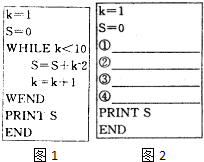 图1给出一个用“当型”循环语句编写的程序:
图1给出一个用“当型”循环语句编写的程序: