题目内容
一个袋中有四个形状大小完全相同的球，球的编号分别为1，2，3，4，先从袋中随机抽取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n．求m+2≤n的概率．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：有放回的取球，根据分步计数原理可知有16种结果，满足条件的情况列举出来，再由古典概型即可得到答案．
解答：
解：先从袋中随机取一个球，该球的编号为m，
将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，
其一切结果（m，n）有4×4=16个
而满足条件m+2≤n的事件有（1，3），（1，4），（2，4）三种结果，
所以满足条件m+2≤n的概率为P=
．
将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，
其一切结果（m，n）有4×4=16个
而满足条件m+2≤n的事件有（1，3），（1，4），（2，4）三种结果，
所以满足条件m+2≤n的概率为P=
| 3 |
| 16 |
点评：本小题主要考查古典概概型，考查学生分析问题、解决问题的能力．能判断一个试验是否是古典概型，分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
已知tanα=-
，sinβ=
，β∈（
，π），则tan（2α-β）=（ ）
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某几何体的三视图如图所示，当xy最大时，该几何体的体积为（ ）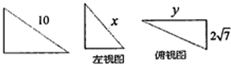
A、2
| ||
B、4
| ||
C、8
| ||
D、16
|
“-3＜m＜-1”是方程
+
=1表示双曲线的（ ）
| x2 |
| 2+m |
| y2 |
| m+1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在2014年清明节期间，高速公路车辆较多，某调查公司在服务区从七座以下小型汽车中，按进服务区的先后每间隔50辆就抽取一辆的抽样方法，抽取40名驾驶员进行调查，将他们在某段高速公路上的车速（km/h）分成6段：（60，65），[65，70），[70，75），[80，85），[85，90）后得到如图的频率分布直方图．