题目内容
在△ABC中,已知tanA•tanB>1,则△ABC是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、最小内角大于45°的三角形 |
考点:正弦定理
专题:计算题,解三角形
分析:由条件可知A、B均为锐角,化切为弦可得cosC>0,从而判断C也为锐角.
解答:
解:在△ABC中,由tanA•tanB>1>0,知A、B均为锐角,
tanA•tanB>1即
•
>1,
∴sinAsinB>cosAcosB,即cos(A+B)<0,-cosC<0,
∴cosC>0,则C也为锐角,
故选:C.
tanA•tanB>1即
| sinA |
| cosA |
| sinB |
| cosB |
∴sinAsinB>cosAcosB,即cos(A+B)<0,-cosC<0,
∴cosC>0,则C也为锐角,
故选:C.
点评:该题考查正弦定理及其应用,考查两角和的余弦函数,属基础题.

练习册系列答案
相关题目
已知tanα=-
,sinβ=
,β∈(
,π),则tan(2α-β)=( )
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知a=log1.20.3,b=log1.20.8,c=1.50.5,则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
设a∈R,若函数y=ex+3ax,x∈R有大于零的极值点,则( )
| A、a>-3 | ||
| B、a<-3 | ||
C、a>-
| ||
D、a<-
|
已知数列{an}满足的前n项和Sn=n2+n+1,那么它的通项公式为an=( )
| A、an=n+1 | |||||
B、an=
| |||||
| C、an=2n | |||||
D、an=
|
某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )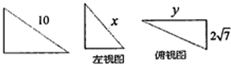

A、2
| ||
B、4
| ||
C、8
| ||
D、16
|
“-3<m<-1”是方程
+
=1表示双曲线的( )
| x2 |
| 2+m |
| y2 |
| m+1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |