题目内容
2.等差数列{an}的前n项和为Sn,且a1<0,若存在自然数m≥3,使得am=Sm,则当n>m时,Sn与an的大小关系是( )| A. | Sn<an | B. | Sn≤an | C. | Sn>an | D. | 大小不能确定 |
分析 推导出Sm-1=0,从而am-1=-a1>0,等差数列{an}的公差d>0,当n>m时,an>0,由此能求出结果.
解答 解:∵Sm=Sm-1+am=am,
∴Sm-1=0,即,又m≥3,a1<0,
∴am-1=-a1>0,
∴等差数列{an}的公差d>0,
∴当n>m时,an>0,
∴Sn=Sm-1+am+am+1+…+an>an.
故选:C.
点评 本题考查当n>m时,Sn与an的大小关系的判断,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
12.设复数z满足i3=z(1-i)(i为虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.数列{an}中,如果an=49-2n,则Sn取最大值时,n等于( )
| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
10.已知函数f(x)是定义在R上的奇函数,且在(0,+∞)上单调递增,若f(-1)=0,则不等式f(2x-1)>0解集为( )
| A. | $({0,\frac{1}{2}})∪({1,+∞})$ | B. | $({-∞,\frac{1}{2}})∪({1,+∞})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})$ |
17.如图为某几何体的三视图,则该几何体的外接球的表面积为( )
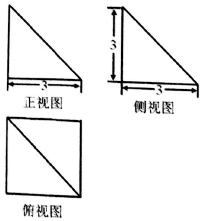

| A. | $\frac{27}{2}π$ | B. | 27π | C. | 27$\sqrt{3}$π | D. | $\frac{27\sqrt{3}π}{2}$ |
7.已知函数f(x)=$\left\{\begin{array}{l}f(x-5),x>2\\ a{e^x},-2≤x≤2\\ f(-x),x<-2\end{array}$,若f(-2016)=e2,则a=( )
| A. | e | B. | 1 | C. | -1 | D. | -e |
11.定义域在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}({x+1}),0≤x<1\\ 1-|{x-3}|,x≥1\end{array}$,则关于x的方程f(x)-a=0(0<a<1)所有根之和为1-$\sqrt{2}$,则实数a的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{4}$ |