题目内容
11.定义域在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}({x+1}),0≤x<1\\ 1-|{x-3}|,x≥1\end{array}$,则关于x的方程f(x)-a=0(0<a<1)所有根之和为1-$\sqrt{2}$,则实数a的值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{4}$ |
分析 由题意,作函数y=f(x)与y=a的图象,从而可得x1+x2=-6,x4+x5=6,x3=1-2a,从而解得.
解答 解:由题意,作函数y=f(x)与y=a的图象如下,
结合图象,
设函数F(x)=f(x)-a(0<a<1)的零点分别为
x1,x2,x3,x4,x5,
则x1+x2=-6,x4+x5=6,
-log0.5(-x3+1)=a,
x3=1-2a,
故x1+x2+x3+x4+x5=-6+6+1-2a=1-2a,
∵关于x的方程f(x)-a=0(0<a<1)所有根之和为1-$\sqrt{2}$,
∴a=$\frac{1}{2}$.
故选B.
点评 本题考查了数形结合的思想应用及函数的性质应用,属于中档题.

练习册系列答案
相关题目
2.等差数列{an}的前n项和为Sn,且a1<0,若存在自然数m≥3,使得am=Sm,则当n>m时,Sn与an的大小关系是( )
| A. | Sn<an | B. | Sn≤an | C. | Sn>an | D. | 大小不能确定 |
6.若$tan({α+\frac{π}{4}})=-3$,则cos2α+2sin2α=( )
| A. | $\frac{9}{5}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | 0 |
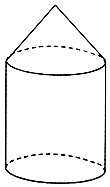 如图,某粮仓是由圆柱和圆锥构成(粮仓的底部位于地面上),圆柱的底面直径与高都等于h米,圆锥的高为$\frac{1}{2}$h米.
如图,某粮仓是由圆柱和圆锥构成(粮仓的底部位于地面上),圆柱的底面直径与高都等于h米,圆锥的高为$\frac{1}{2}$h米.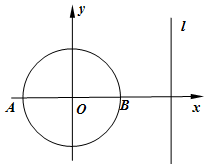 如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.
如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.