题目内容
14．解不等式：（1）x2-2x-3＞0
（2）$\frac{x-2}{x-1}$≤0．
分析 （1）由x2-2x-3＞0 可得（x-3）（x+1）＞0，可得（x-3）＞0且（x+1）＞0或（x-3）＜0且（x+1）＜0，可得答案．
（2）根据分式不等式$\frac{x-2}{x-1}$≤0等价于（x-2）（x-1）≤0且（x-1）≠0可得答案．
解答 解：（1）x2-2x-3＞0 可得（x-3）（x+1）＞0，可得（x-3）＞0且（x+1）＞0或（x-3）＜0且（x+1）＜0，
解得：x＞3或x＜-1．
故得不等式的解集为：{x|x＞3或x＜-1}
（2）（2）$\frac{x-2}{x-1}$≤0等价于（x-2）（x-1）≤0且（x-1）≠0，
解得：1＜x≤2．
故得不等式的解集为：{x|1＜x≤2}．
点评 二次不等式，分式不等式的解法，体现了等价转化数学思想，比较基础．
练习册系列答案
相关题目
4．设f（x）是定义在R上的偶函数，对x∈R，都有f（x-2）=f（x+2），且当x∈[-2，0]时，f（x）=（$\frac{1}{2}$）x-1，若在区间[-2，6]内关于x的方程f（x）-loga（x+2）=0（a＞1）恰有3个不同实根，则a的取值范围是（ ）
| A． | $\root{3}{4}$＜a＜2 | B． | 1＜a＜2 | C． | $\root{3}{4}$＜a＜$\root{6}{9}$ | D． | 1＜a＜$\root{3}{7}$ |
2．等差数列{an}的前n项和为Sn，且a1＜0，若存在自然数m≥3，使得am=Sm，则当n＞m时，Sn与an的大小关系是（ ）
| A． | Sn＜an | B． | Sn≤an | C． | Sn＞an | D． | 大小不能确定 |
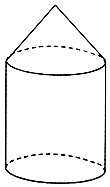如图，某粮仓是由圆柱和圆锥构成（粮仓的底部位于地面上），圆柱的底面直径与高都等于h米，圆锥的高为$\frac{1}{2}$h米．
6．若$tan（{α+\frac{π}{4}}）=-3$，则cos2α+2sin2α=（ ）
| A． | $\frac{9}{5}$ | B． | 1 | C． | $-\frac{3}{5}$ | D． | 0 |