题目内容
12.已知α、β表示两个不同的平面,m为平面α内的一条直线,则“m⊥β”是“α⊥β”的充分不必要条件(选填“充分不必要条件”、“必要不充分条件”、“充要条件”或“既不充分又不必要条件”中的一种).分析 根据充分条件和必要条件的定义,判断即可.
解答 解:∵α、β表示两个不同的平面,m为平面α内的一条直线,
∴“m⊥β,根据判定定理得出:α⊥β”
∵α⊥β”,反之运用平面的垂直的定义得出:m不一定垂直β
∴根据充分必要条件的定义得出:“m⊥β”是“α⊥β”的充分不必要条件
故答案为:充分不必要条件
点评 本题主要考查充分条件和必要条件的应用,直线平面的垂直的定义判断定理是解决本题的关键.

练习册系列答案
相关题目
2.等差数列{an}的前n项和为Sn,且a1<0,若存在自然数m≥3,使得am=Sm,则当n>m时,Sn与an的大小关系是( )
| A. | Sn<an | B. | Sn≤an | C. | Sn>an | D. | 大小不能确定 |
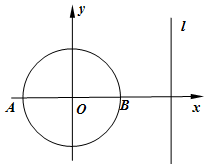 如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.
如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.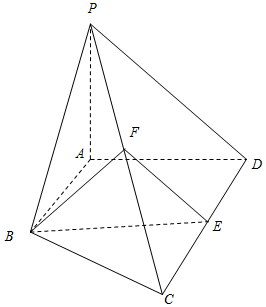 如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.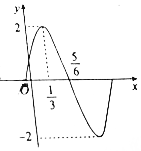 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)